An object of mass 'm' is attached to a vertical fixed spring of spring constant 'k' and is allowed to fall under the gravity. What is the distance traversed by the object before being stopped ?
mg/k
2mg/k
mg/2k
none of these
The correct Answer is:B
To solve the problem of an object of mass 'm' attached to a vertical fixed spring of spring constant 'k' that is allowed to fall under gravity, we will apply the principle of conservation of energy. Here's the step-by-step solution:
Step 1: Understand the Initial and Final Conditions
- Initially, the object is at rest at a height above the spring, and its initial potential energy is due to its height above the ground.
- When the object falls and comes to a stop, it has converted its gravitational potential energy into spring potential energy.
Step 2: Write the Energy Conservation Equation
- The initial gravitational potential energy (PE_initial) when the object is at height 'x' is given by:
PEinitial=mgh=mgx
where 'h' is the height fallen, which is equal to 'x' in this case.
- The potential energy stored in the spring (PE_spring) when it is stretched by 'x' is given by:
PEspring=12kx2
Step 3: Set Up the Equation
- According to the conservation of energy, the total initial energy equals the total final energy:
mgx=12kx2
Step 4: Rearranging the Equation
- Rearranging the equation gives:
12kx2−mgx=0
- Factoring out 'x' from the equation:
x(12kx−mg)=0
Step 5: Solve for 'x'
- This gives us two solutions:
1. x=0 (the trivial solution where the object does not move)
2. 12kx=mg which leads to:
kx=2mg⇒x=2mgk
Step 6: Conclusion
- The distance traversed by the object before being stopped by the spring is:
x=2mgk
- Initially, the object is at rest at a height above the spring, and its initial potential energy is due to its height above the ground.
- When the object falls and comes to a stop, it has converted its gravitational potential energy into spring potential energy.
- The initial gravitational potential energy (PE_initial) when the object is at height 'x' is given by:
PEinitial=mgh=mgx
where 'h' is the height fallen, which is equal to 'x' in this case.
- The potential energy stored in the spring (PE_spring) when it is stretched by 'x' is given by:
PEspring=12kx2
- According to the conservation of energy, the total initial energy equals the total final energy:
mgx=12kx2
- Rearranging the equation gives:
12kx2−mgx=0
- Factoring out 'x' from the equation:
x(12kx−mg)=0
- This gives us two solutions:
1. x=0 (the trivial solution where the object does not move)
2. 12kx=mg which leads to:
kx=2mg⇒x=2mgk
- The distance traversed by the object before being stopped by the spring is:
x=2mgk
Similar Questions

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionA block of mass m hangs an a vertical spring. Initially the spring is unstretched, it is now allowed to fall from rest. Find
(a) the distance the block falls if the block is released slowly,
(b) the maximum distance the block falls before it begins to move up
View Solution
Knowledge Check
An object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
AA√k/mBA2k/mCA√m/kDAm/kA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2km
A block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.

View Solution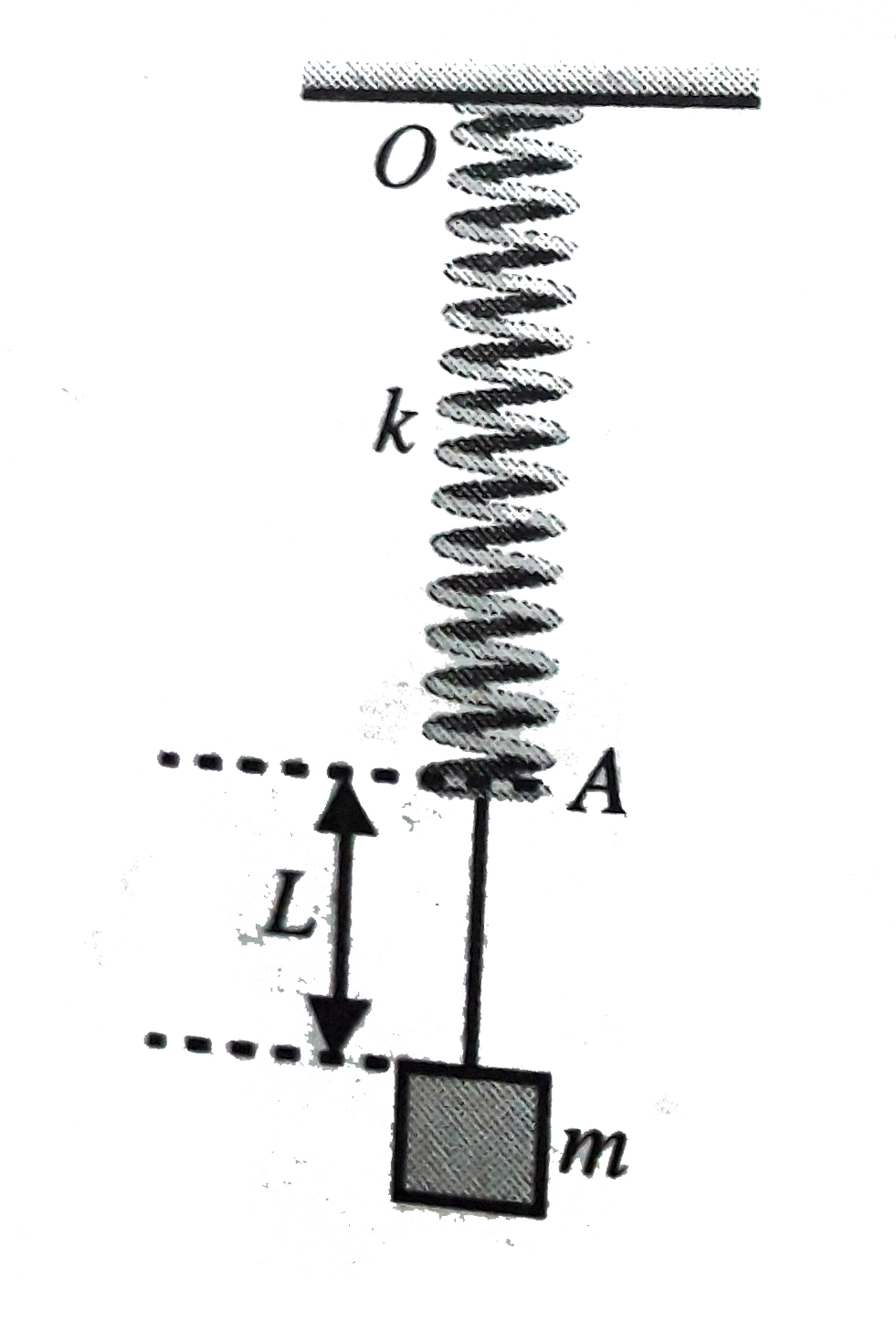
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
Q. If the mass m is now raised up to point A (the top end of the string see fig. and allowed to fall from rest, the maximum extension of the spring in the subsequent motion will be
View SolutionA mass m extends a vertical helical spring of spring constant k by xm at the surface of the earth. Extension in spring by the same mass at height h meter above the surface of the earth is
View Solution

