An explosion blows a rock into three parts. Two pieces go off at right angles to each other. 1.00 kg piece with a velocity 12m/sec and the other 2.00 kg piece with a velocity 8m/sec. If the third piece flies off with a velocity 40m/sec, then the mass of the third piece is -
0.2 kg
0.3 kg
0.4 kg
0.5 kg
The correct Answer is:D
To solve the problem, we will use the principle of conservation of momentum. The total momentum before the explosion must equal the total momentum after the explosion. Since the rock is initially at rest, the total initial momentum is zero.
1. Identify the masses and velocities of the pieces:
- Mass of piece 1 (m1) = 1.00 kg, velocity (v1) = 12 m/s (along the x-axis)
- Mass of piece 2 (m2) = 2.00 kg, velocity (v2) = 8 m/s (along the y-axis)
- Mass of piece 3 (m3) = ?, velocity (v3) = 40 m/s (unknown direction)
2. Set up the momentum equations:
- The total momentum in the x-direction before the explosion is 0.
- The total momentum in the y-direction before the explosion is also 0.
3. Calculate the momentum of the first two pieces:
- Momentum of piece 1 in the x-direction: p1x=m1⋅v1=1.00kg⋅12m/s=12kg m/s
- Momentum of piece 2 in the y-direction: p2y=m2⋅v2=2.00kg⋅8m/s=16kg m/s
4. Express the momentum of the third piece:
- Let the mass of the third piece be m3.
- The momentum of the third piece can be expressed as p3=m3⋅v3.
- Since the third piece is moving at 40 m/s, we can express its momentum in terms of its components. However, since we don't know the direction, we will consider the total momentum.
5. Apply the conservation of momentum:
- In the x-direction:
0=12+m3⋅v3x
- In the y-direction:
0=16+m3⋅v3y
6. Calculate the magnitude of the momentum of the third piece:
- The magnitude of the momentum of the third piece must balance the total momentum of the first two pieces:
m3⋅40=√(12)2+(16)2
- Calculate √(12)2+(16)2:
√144+256=√400=20
7. Set up the equation:
m3⋅40=20
8. Solve for m3:
m3=2040=0.5kg
Final Answer:
The mass of the third piece is 0.5 kg.
- Mass of piece 1 (m1) = 1.00 kg, velocity (v1) = 12 m/s (along the x-axis)
- Mass of piece 2 (m2) = 2.00 kg, velocity (v2) = 8 m/s (along the y-axis)
- Mass of piece 3 (m3) = ?, velocity (v3) = 40 m/s (unknown direction)
- The total momentum in the x-direction before the explosion is 0.
- The total momentum in the y-direction before the explosion is also 0.
- Momentum of piece 1 in the x-direction: p1x=m1⋅v1=1.00kg⋅12m/s=12kg m/s
- Momentum of piece 2 in the y-direction: p2y=m2⋅v2=2.00kg⋅8m/s=16kg m/s
- Let the mass of the third piece be m3.
- The momentum of the third piece can be expressed as p3=m3⋅v3.
- Since the third piece is moving at 40 m/s, we can express its momentum in terms of its components. However, since we don't know the direction, we will consider the total momentum.
- In the x-direction:
0=12+m3⋅v3x
- In the y-direction:
0=16+m3⋅v3y
- The magnitude of the momentum of the third piece must balance the total momentum of the first two pieces:
m3⋅40=√(12)2+(16)2
- Calculate √(12)2+(16)2:
√144+256=√400=20
m3⋅40=20
m3=2040=0.5kg
The mass of the third piece is 0.5 kg.
Similar Questions
An explosion blows a rock into three parts. Two pieces go off at right angles to each other, 1.0kg piece with velocity of 12m/s and other , 1.0kg piece with a velocity of 12m/s and other 2.0kg piece with a velocity of 8m/s. If the third piece flies off with a velocity of 40m/s compute the mass of the third piece.
View SolutionAn explosion blows a rock into three pieces Two pieces whose masses are 200 kg and 100 kg go off at 90∘ to eachother with a velocity of 8m/s and 12m/s respectively If the third piece flies off with a velocity of25m/s then calculate the mass of this piece and indicate the direction of flight of this piece in a diagram.
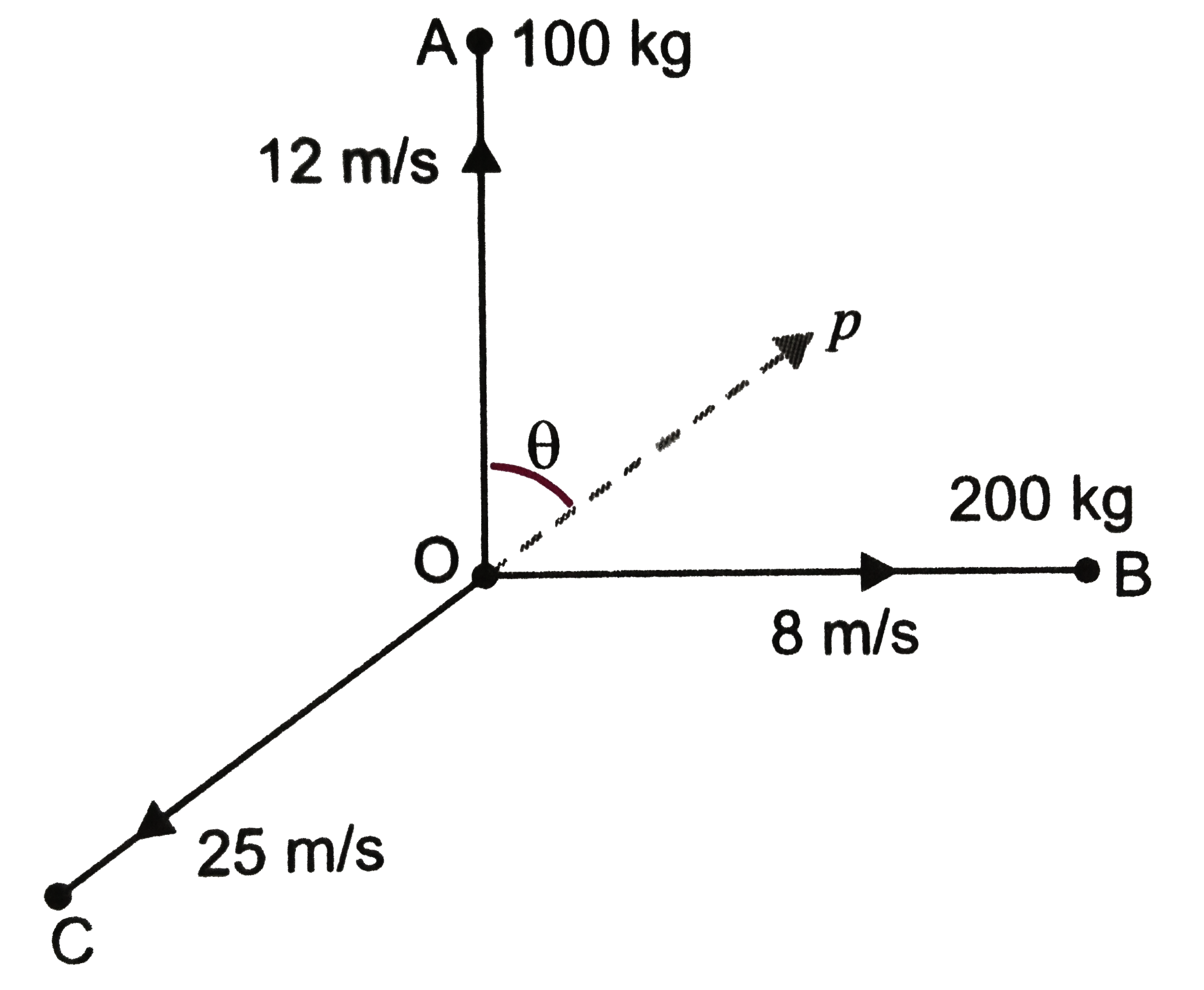
View Solution
Knowledge Check
An explosion blows a rock into three parts. Two parts go off at right angles to each other. These two are, 1 kg first part moving with a velocity of 12ms−1and2kg second part moving with a velocity 8ms−1. If the third part flies off with a velocity of 4 m s^(-1), its mass would be
A7 kgB17 kgC3 kgD5 kgAn explosion blows a rock into three parts. Two parts go off at right angles to each other . These two are 1kg first part moving with a velocity of 12ms−1and2kg second part moving with a velocity of 8ms−1. If the third part flies off with a velocity of 4ms−1. Its mass would be
A5kgB7kgC17kgD3kgA stationary body of mass 3 kg explodes into three equal pieces. Two of the pieces fly off at right angles to each other, one with a velocity 2ˆjm/s and the other with a velocity 3ˆjm/s. If the explosion takes place in 10−5 sec, the average force acting on the third piece in Newtons is:
A(2ˆi+3ˆj)10−5B−(2ˆi+3ˆj)10+5C(3ˆj−2ˆi)10−5D(2ˆj−2ˆi)10−5
An explosion breaks a rock into three parts in a horizontal plane. Two of them go off at right angles to each other . The first part of mass 1kg moves with a speed of 12m/s and the second part of mass 2kg moves with 8m/s. If the third part flies off with 4m/s the speed , then its mass is
View SolutionA stationary body of mass 3 kg explodes into three equal pieces. Two of the pieces fly off at right angles to each other, one with a velocity 2ˆi m/s and the other with a velocity 3ˆj m/s. If the explosion takes place in 10−5 s, the average force acting on the third piece in newton is
View SolutionA stationary body of mass 3kg explodes into three equal pieces.Two of the pieces fly off at right angles to each other, one with a velocity 2ˆim/s and the other with a velocity 3ˆjm/s.If the explosion takes place in 10sec,the average force acting on the third place in Newtons is:
View SolutionA stationary body of mass 3kg explodes into three equal pieces. Two of the pieces fly off at right angles to each other. One with a velocity of 2ˆim/s and the other withl velocity of 3ˆim/s. If the explosion takes place in 10−5 the average force acting on the third piece in newtons
View SolutionAn explosion breaks a rock into three parts in a horizontal plane. Two of them go off at right angles to each other. The first part of mass 1 kg moves with a speed of 12ms−1 and the second part of mass 2 kg moves with 8 ms−1 speed. If the third part flies off with 4ms−1 speed, then its mass is
View Solution

