An 8 kg block of ice, released from rest at the top of a 1.5 m long smooth ramp, slides down and falls with a velocity . Find angle of the ramp with horizontal.
The correct Answer is:1
To find the angle of the ramp with the horizontal, we can use the principles of energy conservation and trigonometry. Here’s a step-by-step solution:
Step 1: Identify the parameters
- Mass of the block (m) = 8 kg (not needed for angle calculation)
- Length of the ramp (L) = 1.5 m
- Final velocity (v) = 2.5 m/s
- Initial velocity (u) = 0 m/s (block is released from rest)
Step 2: Use the principle of conservation of energy
The potential energy (PE) at the top of the ramp will convert into kinetic energy (KE) at the bottom of the ramp.
The potential energy at the top is given by:
PE=mgh
where h is the height of the ramp.
The kinetic energy at the bottom is given by:
KE=12mv2
Setting the potential energy equal to the kinetic energy:
mgh=12mv2
Step 3: Cancel mass (m) from both sides
Since mass (m) appears on both sides, we can cancel it out:
gh=12v2
Step 4: Solve for height (h)
Rearranging the equation gives:
h=v22g
Substituting v=2.5m/s and g=9.81m/s2:
h=(2.5)22×9.81
h=6.2519.62
h≈0.318m
Step 5: Use trigonometry to find the angle (θ)
In a right triangle formed by the ramp:
- The length of the ramp (hypotenuse) = 1.5 m
- The height (opposite side) = 0.318 m
Using the sine function:
sin(θ)=hL
sin(θ)=0.3181.5
sin(θ)≈0.212
Step 6: Calculate the angle (θ)
Now, take the inverse sine to find the angle:
θ=sin−1(0.212)
Calculating this gives:
θ≈12.2∘
Final Answer
The angle of the ramp with the horizontal is approximately 12∘.
---
- Mass of the block (m) = 8 kg (not needed for angle calculation)
- Length of the ramp (L) = 1.5 m
- Final velocity (v) = 2.5 m/s
- Initial velocity (u) = 0 m/s (block is released from rest)
The potential energy (PE) at the top of the ramp will convert into kinetic energy (KE) at the bottom of the ramp.
PE=mgh
where h is the height of the ramp.
KE=12mv2
mgh=12mv2
Since mass (m) appears on both sides, we can cancel it out:
gh=12v2
Rearranging the equation gives:
h=v22g
h=(2.5)22×9.81
h=6.2519.62
h≈0.318m
In a right triangle formed by the ramp:
- The length of the ramp (hypotenuse) = 1.5 m
- The height (opposite side) = 0.318 m
sin(θ)=hL
sin(θ)=0.3181.5
sin(θ)≈0.212
Now, take the inverse sine to find the angle:
θ=sin−1(0.212)
Calculating this gives:
θ≈12.2∘
The angle of the ramp with the horizontal is approximately 12∘.
Similar Questions
A block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest

View SolutionA block of mass m is released from the top of fixed inclined smooth plane. if theta is the angle of inclination then vertical accelertion of block is
View Solution
Knowledge Check
A block released from rest from the top of a smooth inclined plane of angle θ1 reaches the bottom in time t1. The same block released from rest from the top of another smooth inclined plane of angle θ2 reaches the bottom in time t2 If the two inclined planes have the same height, the relation between t1andt2 is
At2t1=(sinθ1sinθ2)1/2Bt2t1=1Ct2t1=sinθ1sinθ2Dt2t1=sin2θ1sin2θ2A block released from rest from the top of a smooth inclined plane of angle θ1 reaches the bottom in time t1. The same block released from rest from the top of another smooth inclined plane of angle θ2 reaches the bottom in time t2 If the two inclined planes have the same height, the relation between t1andt2 is
At2t1=(sinθ1sinθ2)1/2Bt2t1=1Ct2t1=sinθ1sinθ2Dt2t1=sin2θ1sin2θ2A block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
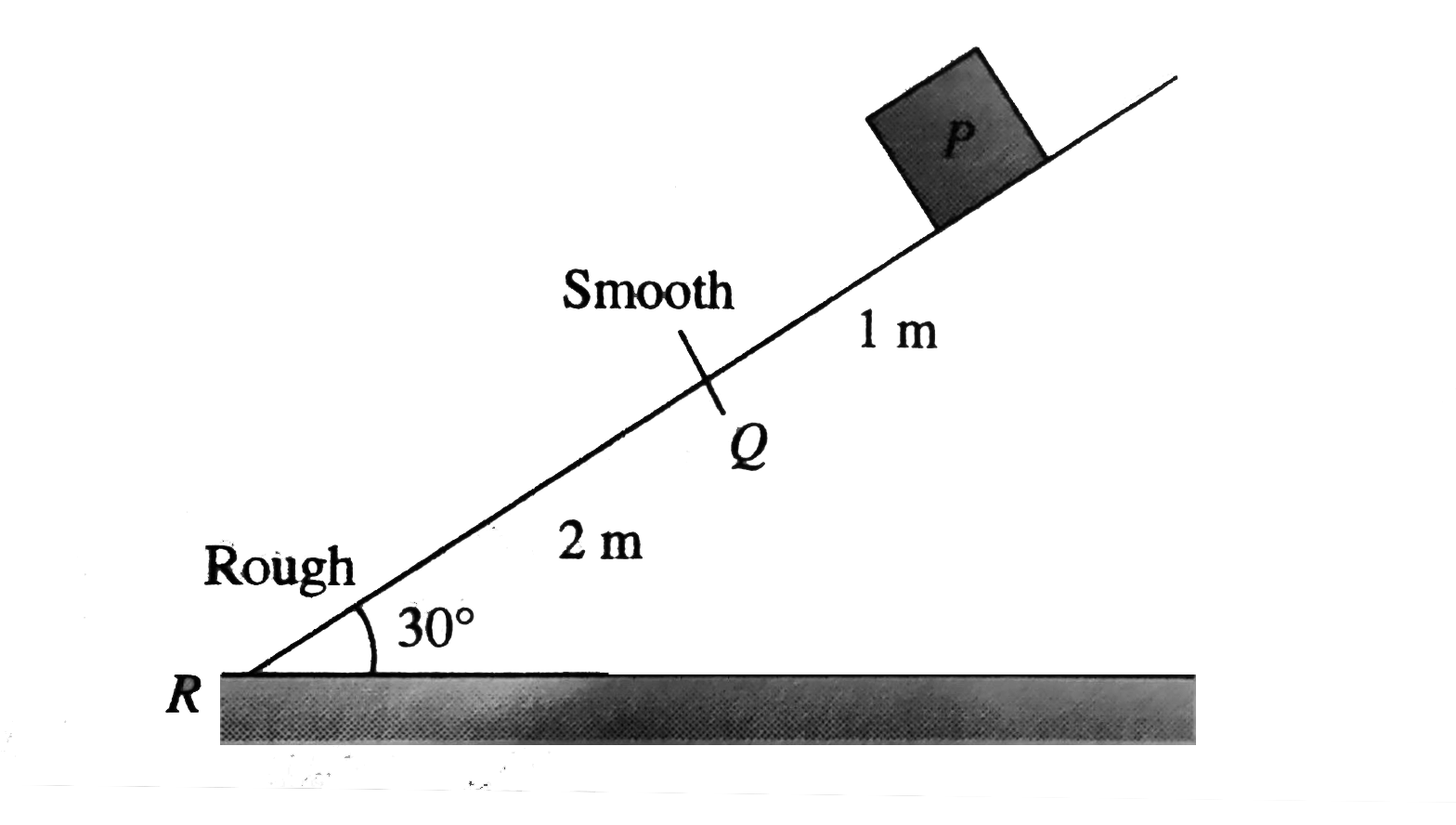 A(a) 2√3B(b) √32C(c) √34D(d) √35
A(a) 2√3B(b) √32C(c) √34D(d) √35
A uniform hoop, disk, and sphere, with the same mass M and same radius R, are released simultaneously from rest at the top of a ramp of length L = 2.5 m and angle θ=12∘ with the horizontal. The objects roll smoothly down the ramp.
What is vcom for each object at the bottom of the ramp?
View SolutionA uniform hoop, disk, and sphere, with the same mass M and same radius R, are released simultaneously from rest at the top of a ramp of length L = 2.5 m and angle θ=12∘ with the horizontal. The objects roll smoothly down the ramp.
(a) Which object wins the race to the bottom of the ramp?
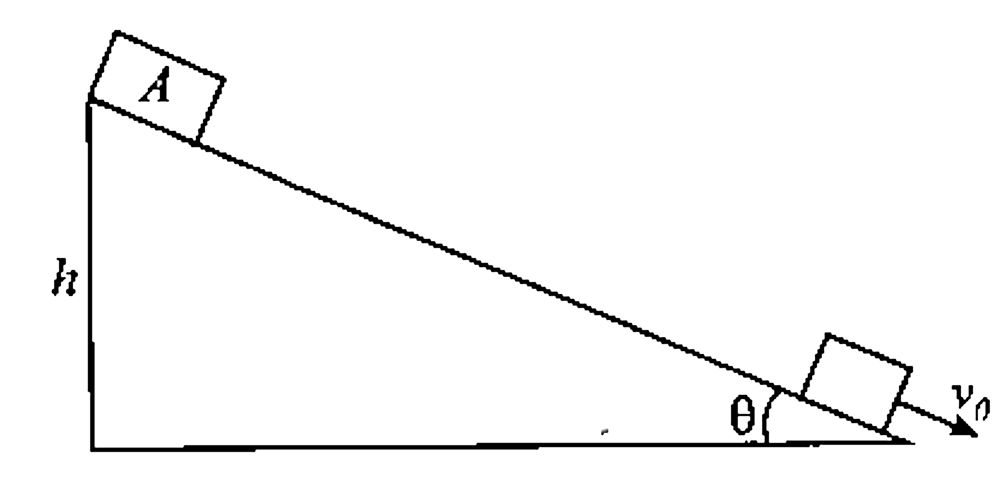
View SolutionA block of A is released from rest from the top of wedge block of height h shown in figure-4.55. If velocity of block when it reaches the bottom of inclive is v0, find the time os sliding.
View SolutionThe three blocks in figure-2.25 are released from rest and accelerate at the rate of 5m/s2. If M = 4kg, what is the magnitude of the frictional force on the block that slides horizontally?
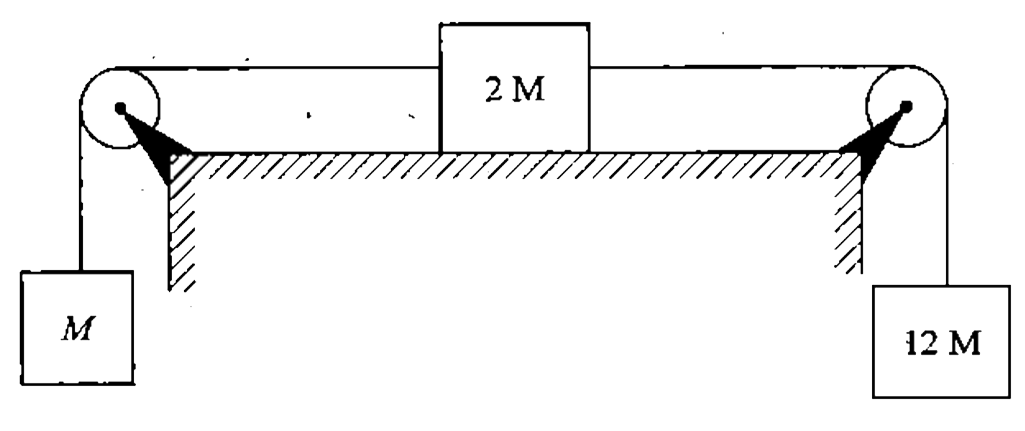
[140 N]
View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100M/m and block comes to rest after compressiong spring by 1 m, find the distance travelled by the block before it comes t o rest.

View Solution
