Two bodies of masses m1andm2 fall from heights h1andh2 respectively. The ratio of their velocities when the hit the ground is
(h1)(h2)
√h1√h2
m1h1m2h2
h21h22
The correct Answer is:B
To find the ratio of the velocities of two bodies falling from different heights, we can use the equations of motion under gravity. Here’s a step-by-step solution:
Step 1: Understand the problem
We have two bodies with masses m1 and m2 falling from heights h1 and h2 respectively. We need to find the ratio of their velocities when they hit the ground.
Step 2: Use the equation of motion
For an object falling freely under gravity, the final velocity V can be calculated using the equation:
V2=U2+2gh
where:
- V = final velocity
- U = initial velocity (which is 0 for free fall)
- g = acceleration due to gravity (approximately 9.81m/s2)
- h = height from which the object is falling
Since the initial velocity U=0, the equation simplifies to:
V2=2gh
Step 3: Calculate the final velocities
For the first body falling from height h1:
V21=2gh1
For the second body falling from height h2:
V22=2gh2
Step 4: Find the ratio of the velocities
To find the ratio of the velocities V1 and V2, we take the square root of the ratio of their squares:
V21V22=2gh12gh2=h1h2
Thus, we have:
V1V2=√h1h2
Step 5: Final result
The ratio of the velocities of the two bodies when they hit the ground is:
V1V2=√h1h2
We have two bodies with masses m1 and m2 falling from heights h1 and h2 respectively. We need to find the ratio of their velocities when they hit the ground.
For an object falling freely under gravity, the final velocity V can be calculated using the equation:
V2=U2+2gh
where:
- V = final velocity
- U = initial velocity (which is 0 for free fall)
- g = acceleration due to gravity (approximately 9.81m/s2)
- h = height from which the object is falling
V2=2gh
For the first body falling from height h1:
V21=2gh1
For the second body falling from height h2:
V22=2gh2
To find the ratio of the velocities V1 and V2, we take the square root of the ratio of their squares:
V21V22=2gh12gh2=h1h2
Thus, we have:
V1V2=√h1h2
The ratio of the velocities of the two bodies when they hit the ground is:
V1V2=√h1h2
Similar Questions
Two bodies A (of mass 1 kg ) and B (of mass 3kg ) are dropped from heights of 16m and 25m ,respectively What is the ratio of the times taken by them to reach the ground?
View Solutiontwo bodies A and B of equal masses are kept at heights of h and 2h respectively. What will be the ratio of their potential energies ?
View Solution
Knowledge Check
Two bodies of masses (m1) and (m2) are droppded from heithts h1 and h2, respectively. They reach the ground after time t1 and t2 and strike the ground with v1 and v2, respectively Choose the correct relations from the following.
At1t2=√h1h2Bt1t2=√h2h1Cv1v2=√h1h2Dv1v2=h2h1Two bodies A (of mass 1kg) and B (of mass 3kg) are dropped from heights of 16m and 25m. Respectively. The ratio of the time taken to reach the ground is :
A5/4B12/5C5/12D4/5Two bodies of different masses are dropped from height of 16 m and 25 m respectively. The ratio of the times taken by them is
A2516B1625C54D45
Two spherical bodies of mass m1 & m2 are having radius 1 m & 2 m respectively. The gravitational field of the two bodies with their radial distance is shown below. The value of m1m2 is
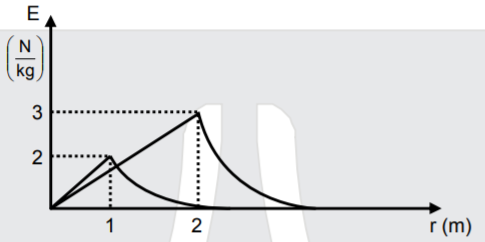 -
-
View SolutionTwo bodies of equal weight are kept at heights of h and 1.5 h respectively. The ratio of their P.E. is
View SolutionTwo bodies having masses in the ratio 2:3 fall freely under gravity from heights 9:16. The ratio of their linear momenta on touching, the ground is
View SolutionTwo bodies having masses in the ratio 2:3 fall freely under gravity from heights 9:16. The ratio of their linear momenta on touching, the ground is
View SolutionTwo bodies of masses m1 and m2(m1=2m2) are dropped from a height. The ratio of time taken by them to reach the ground is ________.
View Solution

