Three equal masses of 1 kg each are placed at the vertices of an equilateral triangle PQR and a mass of 2 kg is placed at the centroid O of the triangle which is at a distance of √2m from each of the vertices of the triangle. The force, in newton, acting on the mass of 2 kg is :
2
1
3
zero
The correct Answer is:D
To solve the problem, we need to calculate the gravitational force acting on the 2 kg mass placed at the centroid O of the equilateral triangle formed by the three 1 kg masses at vertices P, Q, and R.
1. Identify the Forces Acting on the 2 kg Mass:
The three 1 kg masses at the vertices P, Q, and R exert gravitational forces on the 2 kg mass at the centroid O. The gravitational force between two masses is given by the formula:
F=G⋅m1⋅m2r2
where G is the gravitational constant, m1 and m2 are the masses, and r is the distance between them.
2. Calculate the Force from One Mass:
For each of the 1 kg masses (let's denote one of them as m1=1kg) acting on the 2 kg mass (m2=2kg), and given that the distance r=√2m:
F1=G⋅1⋅2(√2)2=G⋅22=G
Thus, the force exerted by each 1 kg mass on the 2 kg mass is G.
3. Determine the Direction of the Forces:
Since the triangle is equilateral, the angles between the forces exerted by the three masses at the centroid will be 120 degrees. Therefore, we have three forces F1,F2,F3 acting at angles of 120 degrees to each other.
4. Use Lami's Theorem:
According to Lami's theorem, if three forces are acting at a point and are in equilibrium, the following relationship holds:
F1sin(α)=F2sin(β)=F3sin(γ)
Here, α=β=γ=120∘. Since all forces are equal (F1=F2=F3=G), we can conclude that:
Gsin(120∘)=Gsin(120∘)=Gsin(120∘)
This confirms that the net force acting on the 2 kg mass is zero.
5. Conclusion:
Since the net force acting on the mass of 2 kg at the centroid O is zero due to the symmetry and equal magnitudes of the forces, we conclude:
Net Force=0N
Final Answer:
The force acting on the mass of 2 kg is 0 N.
The three 1 kg masses at the vertices P, Q, and R exert gravitational forces on the 2 kg mass at the centroid O. The gravitational force between two masses is given by the formula:
F=G⋅m1⋅m2r2
where G is the gravitational constant, m1 and m2 are the masses, and r is the distance between them.
For each of the 1 kg masses (let's denote one of them as m1=1kg) acting on the 2 kg mass (m2=2kg), and given that the distance r=√2m:
F1=G⋅1⋅2(√2)2=G⋅22=G
Thus, the force exerted by each 1 kg mass on the 2 kg mass is G.
Since the triangle is equilateral, the angles between the forces exerted by the three masses at the centroid will be 120 degrees. Therefore, we have three forces F1,F2,F3 acting at angles of 120 degrees to each other.
According to Lami's theorem, if three forces are acting at a point and are in equilibrium, the following relationship holds:
F1sin(α)=F2sin(β)=F3sin(γ)
Here, α=β=γ=120∘. Since all forces are equal (F1=F2=F3=G), we can conclude that:
Gsin(120∘)=Gsin(120∘)=Gsin(120∘)
This confirms that the net force acting on the 2 kg mass is zero.
Since the net force acting on the mass of 2 kg at the centroid O is zero due to the symmetry and equal magnitudes of the forces, we conclude:
Net Force=0N
The force acting on the mass of 2 kg is 0 N.
Similar Questions
Three equal masses of 1 kg each are placed at the vertices of an equilateral ΔPQR and a mass of 2kg is placed at the centroid O of the triangle which is at a distance of √2m from each the verticles of the triangle. Find the force (in newton) acting on the mass of 2 kg.
View SolutionThree masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View Solution
Knowledge Check
Three equal masses of 2kg each are placed at the vertices of an equilateral triangle and a mass of 4 kg is placed at the centroid of the triangle which is at a distance of √2 m from each of the vertices of the triangle. The force, (in newton) acting on the mass of 4 kg is
A2B√2C1DzeroThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle which is at a distance of sqr(2) m from each of the vertices of the triangle .The force . In newton , acting on the mass of 2 kg is
A2B1C1DZeroThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
A{6.67(10−11)}NB10−3 NC[11.5(10−11)]ND[11.5(10−3)]N
Two balls of mass m each are placed at the two vertices of an equilateral triangle. Another ball of mass 2m is placed at the third vertex of the triangle. Locate the centre of mass of the system.
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
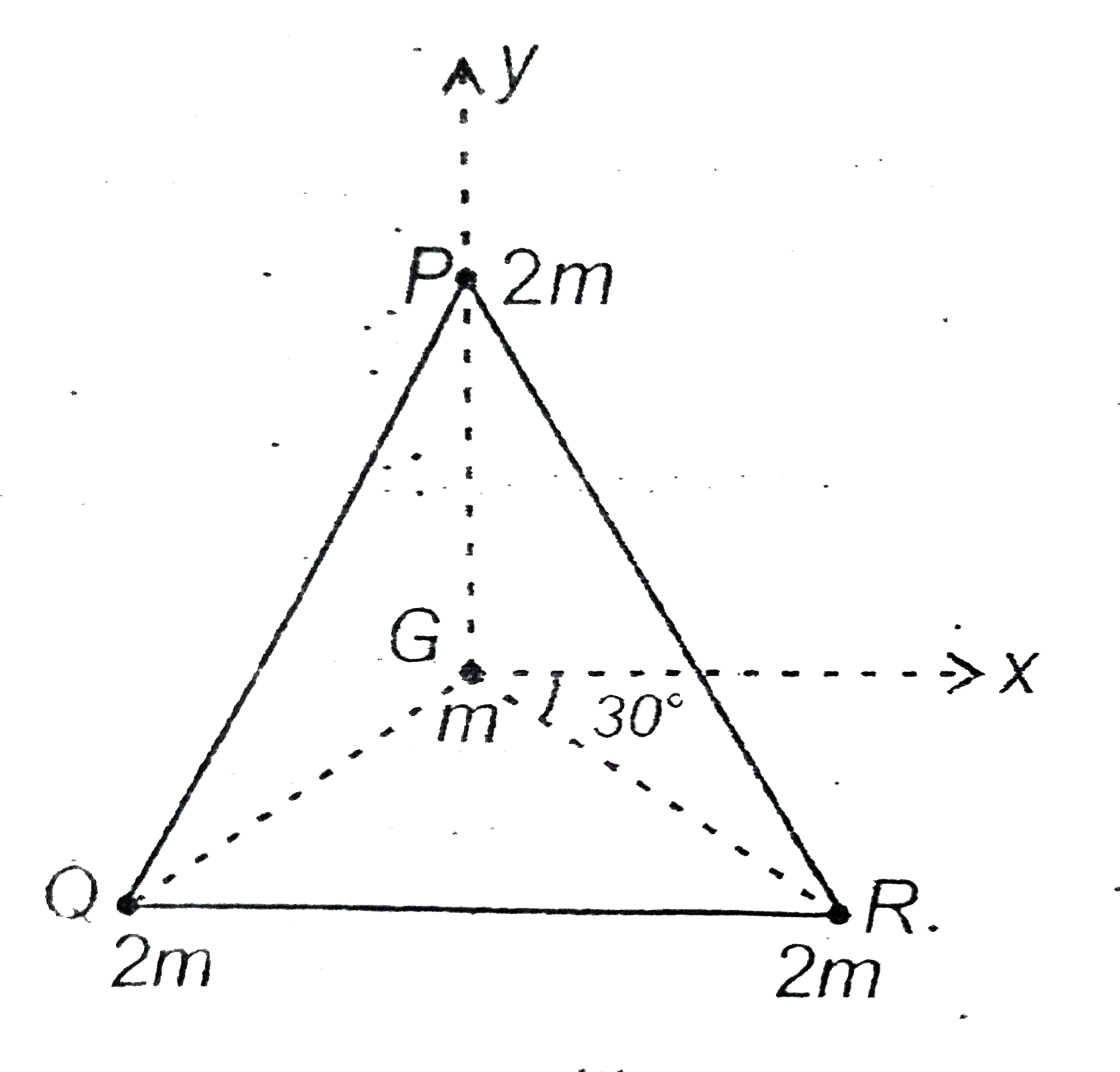
View SolutionThree equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m
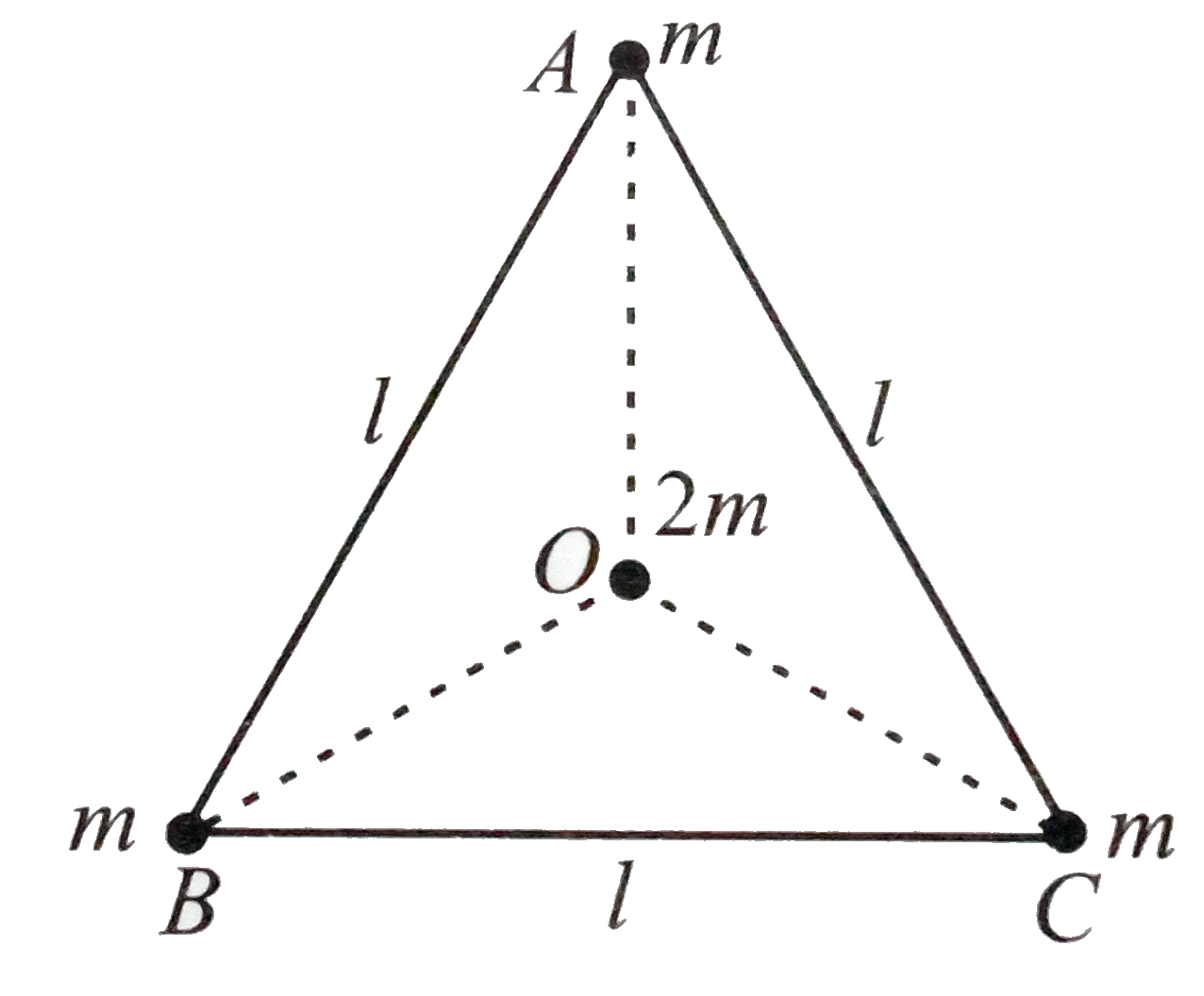
View SolutionThree masses each of mass m are placed at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View Solution

