A boy wants to hold a 50 kg box on a snow covered hill. The hill makes an angle of 30∘ with the horizontal. What force the boy must exert parallel to the slope ?
25 N
245 N
424 N
490 N
The correct Answer is:B
To solve the problem, we need to determine the force that the boy must exert parallel to the slope to hold the box in place. We can break this down into steps:
Step 1: Identify the Forces Acting on the Box
The forces acting on the box include:
1. The gravitational force acting downward (weight of the box).
2. The normal force acting perpendicular to the slope.
3. The force exerted by the boy acting parallel to the slope.
Step 2: Calculate the Weight of the Box
The weight (W) of the box can be calculated using the formula:
W=m⋅g
where:
- m=50kg (mass of the box)
- g=9.81m/s2 (acceleration due to gravity)
Calculating the weight:
W=50kg⋅9.81m/s2=490.5N
Step 3: Resolve the Weight into Components
Since the hill is inclined at an angle of 30∘, we need to resolve the weight into two components:
1. Component parallel to the slope (W∥)
2. Component perpendicular to the slope ( W_{\perpendicular} )
The component of weight acting parallel to the slope is given by:
W∥=W⋅sin(θ)
where θ=30∘.
Calculating W∥:
W∥=490.5N⋅sin(30∘)
Since sin(30∘)=0.5:
W∥=490.5N⋅0.5=245.25N
Step 4: Determine the Force Exerted by the Boy
To hold the box in place, the boy must exert a force equal to the component of the weight acting down the slope. Therefore, the force exerted by the boy (F) is:
F=W∥=245.25N
Conclusion
The force that the boy must exert parallel to the slope to hold the box in place is approximately 245.25N.
---
The forces acting on the box include:
1. The gravitational force acting downward (weight of the box).
2. The normal force acting perpendicular to the slope.
3. The force exerted by the boy acting parallel to the slope.
The weight (W) of the box can be calculated using the formula:
W=m⋅g
where:
- m=50kg (mass of the box)
- g=9.81m/s2 (acceleration due to gravity)
W=50kg⋅9.81m/s2=490.5N
Since the hill is inclined at an angle of 30∘, we need to resolve the weight into two components:
1. Component parallel to the slope (W∥)
2. Component perpendicular to the slope ( W_{\perpendicular} )
W∥=W⋅sin(θ)
where θ=30∘.
W∥=490.5N⋅sin(30∘)
Since sin(30∘)=0.5:
W∥=490.5N⋅0.5=245.25N
To hold the box in place, the boy must exert a force equal to the component of the weight acting down the slope. Therefore, the force exerted by the boy (F) is:
F=W∥=245.25N
The force that the boy must exert parallel to the slope to hold the box in place is approximately 245.25N.
Similar Questions
A force of 400 N acting horizontal pushes u pa 20 kg block placed on a rough inclined plane which makes an angle of 45∘ with the horizontal. The acceleration experienced by the block is 0.6m/s2.Find the coefficient of sliding friction between the box and incline.
View SolutionThe airline passenger in above figure (b) exerts a 80 N force on his suitcase pulling at an angle 60∘ with the horizontal. What work he does on suitcase while pulling it 50 m on the floor ?
View Solution
Knowledge Check
A man pushes a 80 N crate a distance of 5.0 m upward along a frictionless slope that makes an angle of 30∘ with the horizontal. The force he exerts is parallel to the slope. If the speed of the crate increases at a rate of 1.5 then the work done by the man is :
A−200JB61 JC140 JD260 JA car weighing 100kg is on a slope that makes and angle 30∘ with the horizontal. The component of car's weight parallel to the slope is (g=10ms−2)
A500NB1000NC15,000ND20,000NA 63-kg skier goes up a snow-convered hill that makes an angle of 25∘ with the horizontal . The initial speed of the skier is 6.6 m/s. After coasting a distance of 1.9 m up the slope, the speed of the skier is 4.4 m/s. Find the work done by the kinetic frictional force that acts on the skis .
A−760JB+270JC+300JD−270J
Holding on to a tow rope moving parallel to a frictionless ski slope, a 45 kg skier is pulled up the slope, which is at an angle of 8.0∘ with the horizontal. What is the magnitude Frope of the force on the skier from the rope when (a) the magnitude v of the skier's velocity is constant at 2.0 m/s and (b) v = 2.0 m/s as v increases at a rate of 0.10 m/s2 ?
View SolutionA solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of 30∘ with the horizontal. force of friction on the cylinder is?
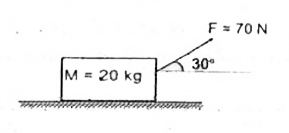
View SolutionA wooden box of mass 20 kg is kept on a rough horizontal surface. The co-efficient of static friction μs=0.41 and co-efficient of kinetic friction μk=0.3 exist between the box and the horizontal surface. A constant force F of 70N is applied to the box at an angle of 30∘ with the horizontal. Find the acceleration of the box on the surface and the frictional force on the box. Take g=10m/s2.
View SolutionA body of mass 10kg is placed on a smooth inclined plane making an angle of 30∘ with the horizontal, the component of the force of gravity trying to move the body down the inclined plane is [g=9.8m/s2]
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution