Let ABCD be a square of side 2a. Find the coordinates of the vertices of this square when (i) A coincides with the origin and AB and AD are along OX and OY respectively. (ii) The centre of the square is at the origin and coordinate axes are parallel to the sides AB and AD respectively
To solve the problem, we will find the coordinates of the vertices of the square ABCD based on the given conditions.
Part (i): A coincides with the origin, and AB and AD are along OX and OY respectively.
1. Identify the coordinates of point A: Since point A coincides with the origin, its coordinates are:
A(0,0)
2. Determine the coordinates of point B: Since AB is along the OX axis and the side length of the square is 2a, point B will be:
B(2a,0)
3. Determine the coordinates of point D: Since AD is along the OY axis, point D will be:
D(0,2a)
4. Determine the coordinates of point C: Point C is diagonally opposite to point A, so its coordinates will be:
C(2a,2a)
Thus, the coordinates of the vertices of square ABCD are:
- A(0,0)
- B(2a,0)
- C(2a,2a)
- D(0,2a)
Part (ii): The center of the square is at the origin, and coordinate axes are parallel to the sides AB and AD respectively.
1. Identify the center of the square: The center of the square is at the origin, which is:
(0,0)
2. Determine the coordinates of point A: Since the side length is 2a, the distance from the center to each vertex is a. Therefore, point A will be:
A(a,a)
3. Determine the coordinates of point B: Since B is to the right of A, its coordinates will be:
B(a,−a)
4. Determine the coordinates of point C: Since C is diagonally opposite to A, its coordinates will be:
C(−a,−a)
5. Determine the coordinates of point D: Since D is to the left of A, its coordinates will be:
D(−a,a)
Thus, the coordinates of the vertices of square ABCD are:
- A(a,a)
- B(a,−a)
- C(−a,−a)
- D(−a,a)
Summary of Coordinates:
1. For part (i):
- A(0,0)
- B(2a,0)
- C(2a,2a)
- D(0,2a)
2. For part (ii):
- A(a,a)
- B(a,−a)
- C(−a,−a)
- D(−a,a)
A(0,0)
B(2a,0)
D(0,2a)
C(2a,2a)
- A(0,0)
- B(2a,0)
- C(2a,2a)
- D(0,2a)
(0,0)
A(a,a)
B(a,−a)
C(−a,−a)
D(−a,a)
- A(a,a)
- B(a,−a)
- C(−a,−a)
- D(−a,a)
1. For part (i):
- A(0,0)
- B(2a,0)
- C(2a,2a)
- D(0,2a)
- A(a,a)
- B(a,−a)
- C(−a,−a)
- D(−a,a)
Topper's Solved these Questions
Similar Questions
ABCD is a square having length of a side 20 units. Taking the centre of the square as the origin and xandy axes parallel to AB and AD respectively, find the coordinates of A, B, C and D.
View SolutionIf (3,−5) and (−1,3) are the coordinates of the opposite vertices of a square then find the equation of its sides and diagonals
View Solution
Knowledge Check
ABCD is a square of side a. The centre of the circle which circumscribes the square on taking AB and AD as axes is
A(a, -a)B(-a, a)C(1/2,a/2)DnoneThe vertices A and D of square ABCD lie on the positive sides of x-axis and y-axis , respectively. If the vertex C is the point (12,17) , then the coordinates of vertex B are
(a)(14,16) (b) (15, 3) 17,5) (d) (17,12)A(14,16)B(15,3)C(17,5)D(17,12)ABCD is a square, the length of whose side is a. Taking AB and AD as the coordinate axes, the equation of the circel passing through the ceteices of the square is
Ax2+y2+ax+ay=0Bx2+y2−ax−ay=0Cx2+y2+1ax+2ay=0Dx2+y2−2ax−2ay=0
A vertex of a square is at the origin and its one side lies along the line 3x-4y-10=0. Find the area of the square.
View SolutionThe center of a square is at the origin and its one vertex is A(2,1). Find the coordinates of the other vertices of the square.
View SolutionABCD is a square . W is the mid point of AB side of square is 16 cm. Find the radius of circle in figure
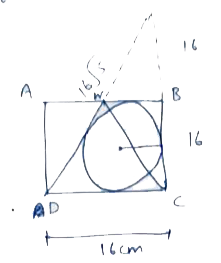
View SolutionEach side of a square is of length 4. The center of of the square is (3,7) and are of its disgonals are parallel to y=x. Then coordinates of the vertices are?
View SolutionThe side of a square ABCD is 'a' units A,B,C,D are in the anti-clockwise order AB and AD are coordinate axes. Then coordinates of C are
View Solution
