In a right triangle BC , right angled at B, the ratio of AB→AC is 1:√2 . Find the values of 2tanA1+tan2A and (ii) 2tanA1−tan2A
Video Solution
Text Solution
Given,
AB:AC=1:√2
⇒ABAC=1√2
So, AB=x and AC=√2x
By Pythagoras theorem, we have
(AC)2=(AB)2+(BC)2
⇒(√2x)2=x2+(BC)2
⇒(BC)2=2x2−x2=x2
⇒BC=x
∴tanA=BCAB=xx=1
(i)2tanA1+tan2A
=2×11+1
=1
(ii) 2tanA1−tan2A
=2×11−1
=0
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a triangle ABC, right angled at C, find the value of tan A + tan B in terms of the sides a,b,c.
Aa2bcBa+bCb2acDc2abIn a right triangle ABC right-angled at B. if tanA=1, then value of 2sinAcosA=.
A0B1C2D3Let triangle ABC be right angled at C.If tanA+tanB2, then-
A∠A=30∘Btriangle ABC must be isosclesCsides of the triangle ABC are 3,4,5Dtriangle must be scalene
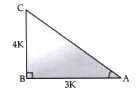
△ABC is a right triangle , right angle at B . Given the ratio of altitude and base tanA=43 . Find the value of (1+tan2A)
View SolutionIn a right triangle ABC right angled at B , ∠ACB=θ , AB=2cm and BC=1 cm . Find the value of sin2θ+tan2θ .
View SolutionIn a △ABC, right-angled at B, if AB : AC = 1:2, then find the value of
2tanA1+tan2A.
View SolutionIf △ABC is a right angled at C, then tanA + tan B equals
View SolutionIn a right triangle ABC, right-angled at B, if sin(A−C)=12 find the measures of angles A and C
View Solution