यदि एक दूसरे से लम्बवत् दो तलों में विचलन कोण (angle of deviation) के मान क्रमशः $δ_{1}$ व $δ_{2}$ मापे जाते हैं जबकि वास्तविक विचलन कोण $δ$ हैं, तो सिद्ध कीजिए की
$\cot^{2} δ_{1} + \cot^{2} δ_{2} = \cot (2) δ$

Video Solution

Text Solution

Verified by Experts

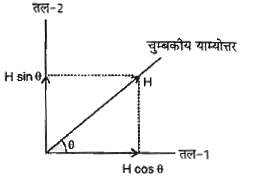
यदि पृथ्वी के चुम्बकत्व का क्षैतिज घटक (horizontal component) H व उर्ध्व घटक (vertical component) V हो, तो
$\tan δ = \frac{V}{H} . . . (i)$
माना चुम्बकीय याम्योत्तर से पहला तल $θ$ कोण बनाता हैं तो पहले तल के लिए पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज घटक $H \cos θ$ होगा अतः वहाँ पर नमन कोण (angle of dip) $δ_{1}$ के लिए
${\tan δ}_{1} = \frac{V}{H \cos θ}$
या $\cos θ = \frac{V}{H {\tan δ}_{1}}$
$∵$ सेमी, (i) से,
$\frac{V}{H} = \tan δ$
$∴ \cos θ = \frac{\tan δ}{{\tan δ}_{1}} . . . (i i)$
इसी प्रकार दूसरे तल के लिए क्षैतिज घटक का मान $H \sin θ$ होगा,
अतः वहाँ नमन कोण $δ_{2}$ के लिए,
${\tan δ}_{2} = \frac{V}{H \sin θ}$
$\Rightarrow \sin θ = \frac{V}{H {\tan δ}_{2}} = \frac{\tan δ}{{\tan δ}_{2}}$
या $\sin θ = \frac{\tan δ}{{\tan δ}_{2}} . . . (i i i)$
समी. (ii) व (iii) के वर्गो को जोड़ने पर,
$\cos^{2} θ + \sin^{2} θ = \frac{\tan^{2} δ}{\tan^{2} δ} = \frac{\tan^{2} δ}{\tan^{2} δ_{2}}$
या $1 = \tan^{2} δ [\frac{1}{\tan^{2} δ_{1}} + \frac{1}{\tan^{2} δ_{2}}]$
या $\frac{1}{\tan^{2} δ} = \frac{1}{\tan^{2} δ_{1}} + \frac{1}{\tan^{2} δ_{2}}$
या $\cot^{2} δ = \cot^{2} δ_{1} + \cot^{2} δ_{2}$

Updated on:21/07/2023

|

Class 12 PHYSICS MAGNETISM AND MATTER

Topper's Solved these Questions

Similar Questions

MITTAL PUBLICATION-चुम्बकत्व एवं चुम्बकीय पदार्थो के गुण-विविध आंकिक उदाहरण

Home
Ask Doubt
Profile