Tony has an A average in his math class and there is one test left. In order to keep the A, he will have to maintain an average test score that is at least 90%. He has completed 5 of the 6 tests and his current average is 91%.Which fo the following scores is th elowest he can earn while still maintaining his A ?
0.8
0.85
0.89
0.9
The correct Answer is:B
To solve the problem step by step, we will follow these calculations:
1. Understanding the Problem: Tony has completed 5 tests with an average score of 91%. He needs to maintain an average of at least 90% after taking one more test.
2. Calculating the Total Score for the First 5 Tests:
- The average score of the first 5 tests is given as 91%.
- The formula for average is:
Average=Sum of scoresNumber of tests
- Let S5 be the sum of the scores of the first 5 tests. Then:
91=S55
- Rearranging gives:
S5=91×5=455
3. Setting Up the Equation for the Average After 6 Tests:
- Let X be the score Tony needs on the 6th test.
- The average score after 6 tests must be at least 90%. Therefore:
Average after 6 tests=S5+X6≥90
- Substituting S5 into the equation:
455+X6≥90
4. Solving the Inequality:
- Multiply both sides by 6 to eliminate the fraction:
455+X≥540
- Now, isolate X:
X≥540−455
- Simplifying gives:
X≥85
5. Conclusion:
- The lowest score Tony can earn on the 6th test while still maintaining his A average is 85.
Summary of Steps:
1. Calculate the total score of the first 5 tests using the average.
2. Set up an equation for the average after 6 tests.
3. Solve the inequality to find the minimum score needed on the last test.
- The average score of the first 5 tests is given as 91%.
- The formula for average is:
Average=Sum of scoresNumber of tests
- Let S5 be the sum of the scores of the first 5 tests. Then:
91=S55
- Rearranging gives:
S5=91×5=455
- Let X be the score Tony needs on the 6th test.
- The average score after 6 tests must be at least 90%. Therefore:
Average after 6 tests=S5+X6≥90
- Substituting S5 into the equation:
455+X6≥90
- Multiply both sides by 6 to eliminate the fraction:
455+X≥540
- Now, isolate X:
X≥540−455
- Simplifying gives:
X≥85
- The lowest score Tony can earn on the 6th test while still maintaining his A average is 85.
1. Calculate the total score of the first 5 tests using the average.
2. Set up an equation for the average after 6 tests.
3. Solve the inequality to find the minimum score needed on the last test.
Similar Questions
Jeff has taken 6 of 1 equally weighted math tests this semester, and he has an average score of exactly 82.0 point. How many points does he need to earn on the 7th test to bring his average score up to exactly 83 points?
View SolutionThe marks scored by Rohit in two tests were 65 and 70. Find the minimum marks he should score in the third test to have an average of at least 65 marks.
View Solution
Knowledge Check
For the first several weeks after hiring a private tutor, Teddy's score on a standardized test increased slowly . As Teddy began to understand the concepts more clearly , though , his standardized test scores improved more rapidly. After several more weeks, Teddy stopped working with his tutor and his scores did not imporve any more . Which of the following graphs could represent all of Teddy's standardized test scores as a function of times , in weeks, after he hired a private tutor ?
A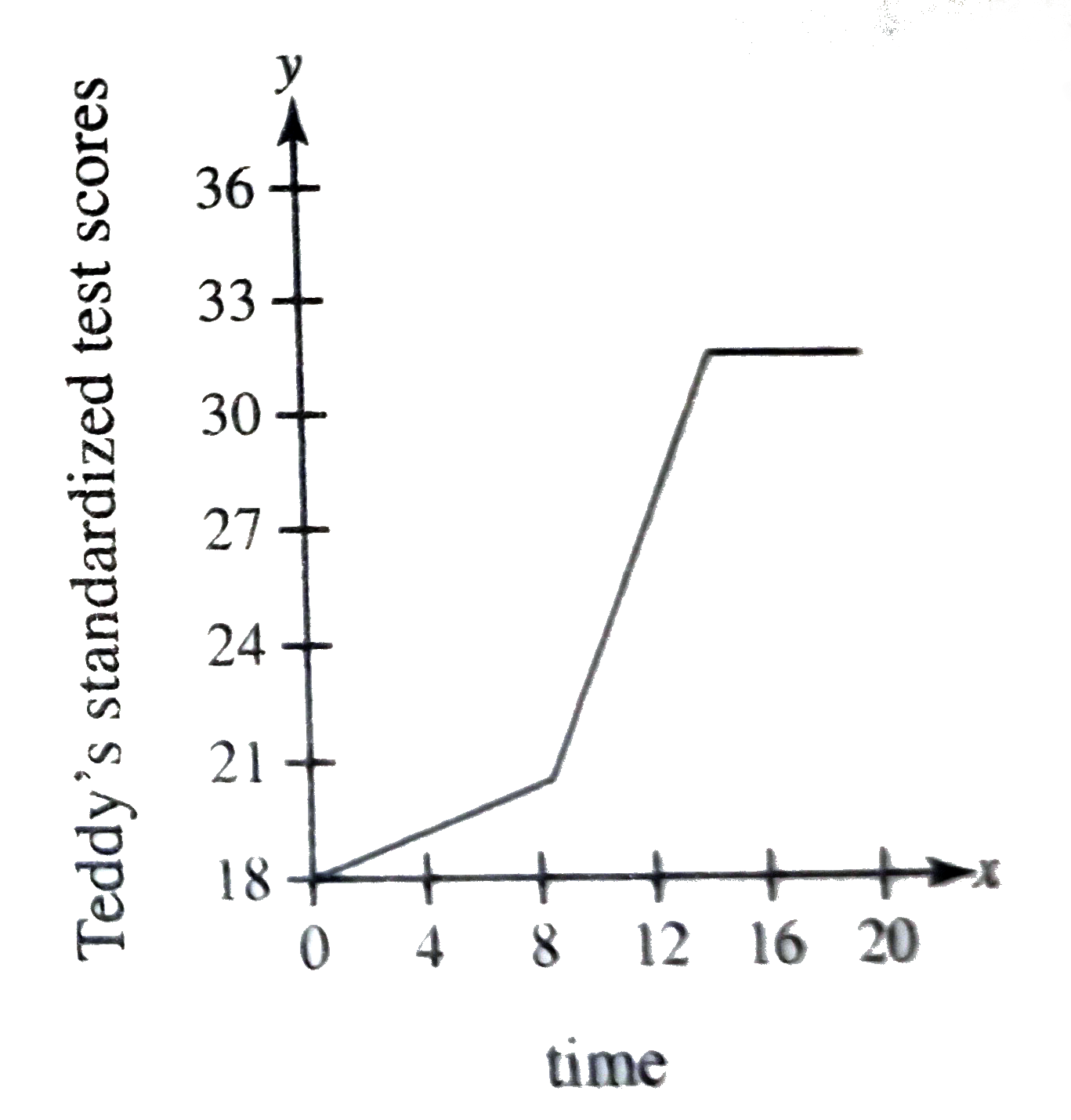 B
B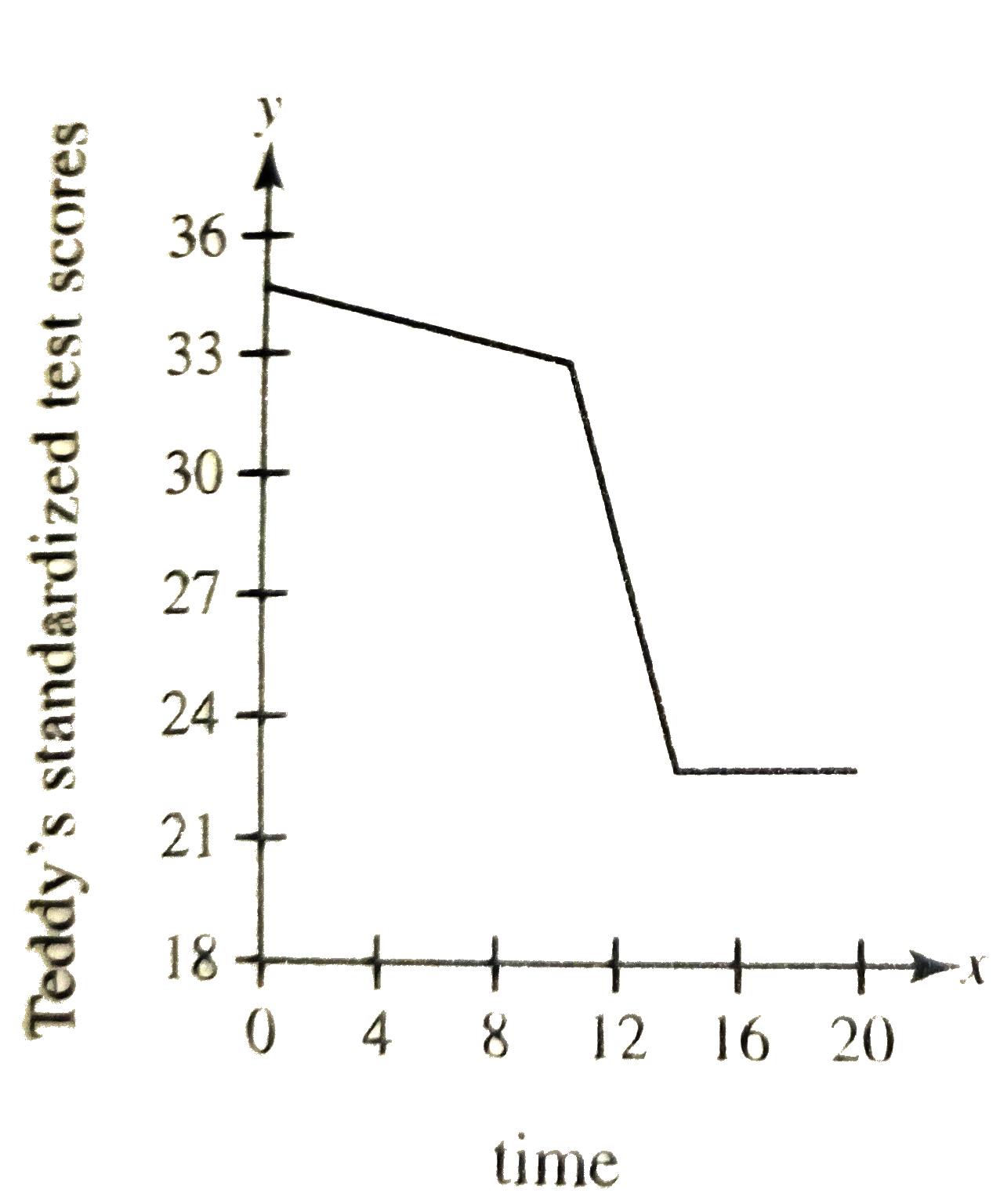 C
C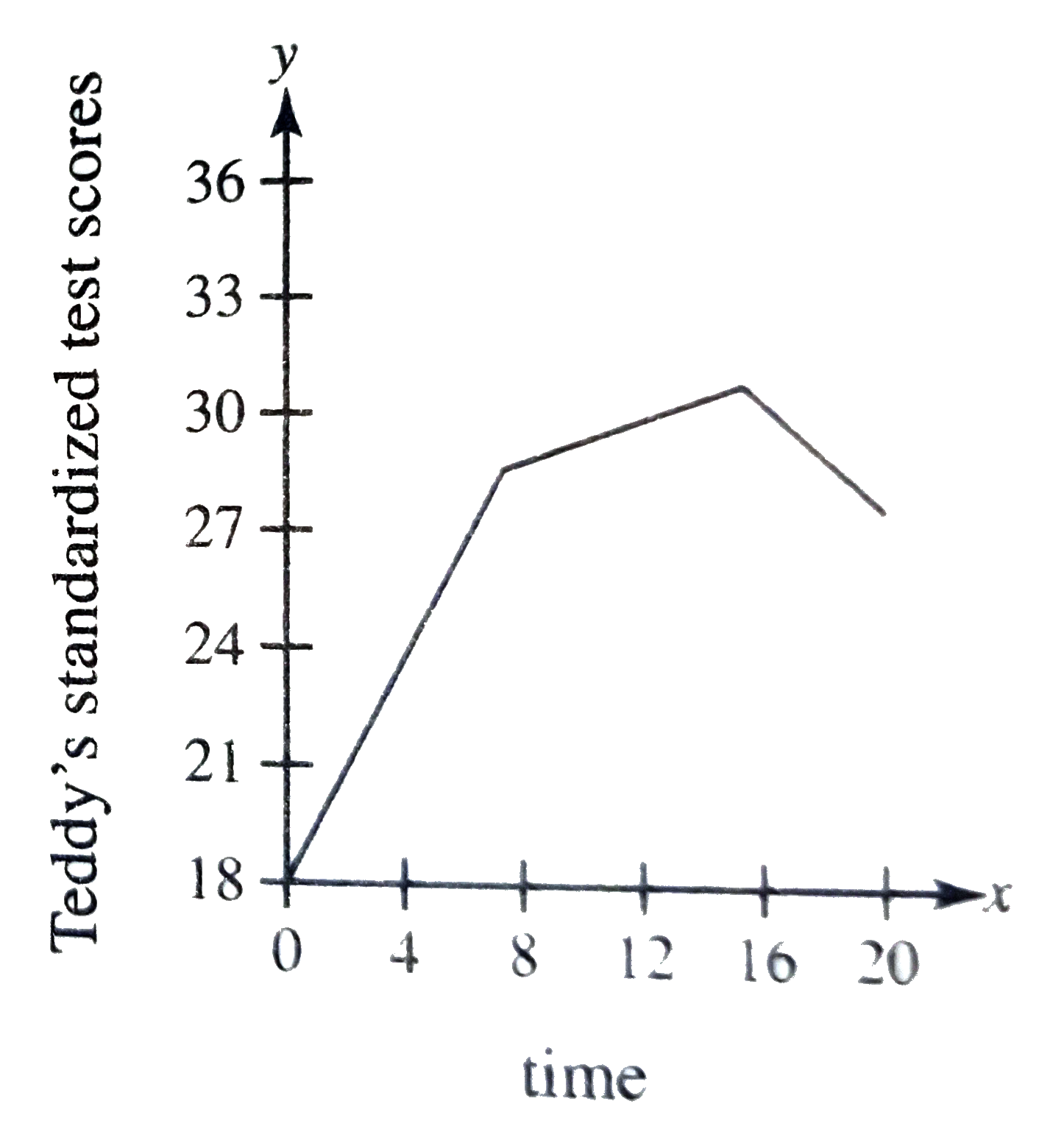 D
D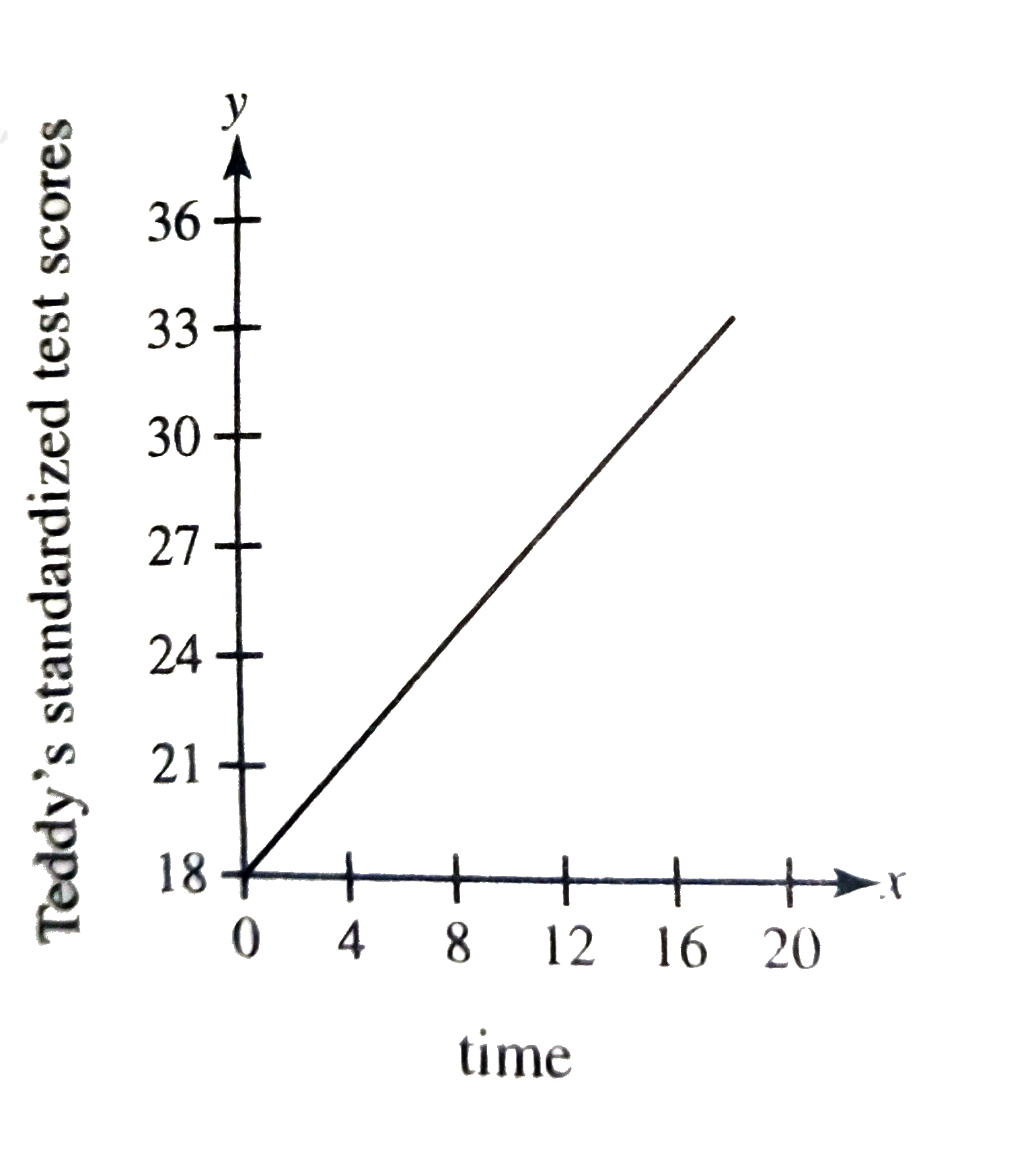
Pete has an average score exactly x points on 4 equally weighted tests. How many points higher than x must Pete score on the 5th equally weighted test to raise his average score after the 5th test to x+2 points?
A2B4C5D10Lennon has 6 hours to spend in Ha Ha Tonka state park. He plants to drive around the park at an average speed of 20 miles per hour, looking for a good trail to hike. Once he finds a trail he likes, he will spend the remainder of his time hiking it. He hopes to travel more than 60 miles total while in the park. If he hikes at an average speed of 1.5 miles per hour, which of the following system of inequalities can be solved for the number of hours Lennon spends driving d, and the number of hours he spends hiking,h, while he is at the park?
A1.5h+20d>60
h+d≤6B1.5h+20d>60
h+d≥6C1.5h+20d<60
h+d≥360D20h+1.5d>6
h+d≤60
Professor Malingowski, a chemist and teacher at to communite college, is organizing his graduated cylinders in the hopes of keeping his office tidy and setting a good example for his students. He has beakers with diameters, in inches, of 12,34,45,1 and 54.
With his original five cylinders, Professor Malingowski realizes that he is missing a cylinder necessary for his upcoming lab demonstration for Thurday's class. He remembers that the cylinder the needs, when added to the original five, will create a median diameter value of 910 for the set of six total cylinders. He also knows that the measure of the sixth cylinder will exceed the value of the range of the current five cylinders by a width of anywhere from 14 inches to 12 inches, inclusive. Based on the above data, which is one possible value of y, the diameter of this missing sixth cylinder?
View SolutionThe overall average grade of a math course is based on homework (10 %) , quizzes (40 %) , and tests (50 %) . Ted has a 90 average for howework , 81 for quizzes , and 85 for tests . What is his overall average ?
View SolutionKalino earned 85, 95, 93 and 80 points on the 4 tests, each worth 100 points, given so far this term. How many points must he earn on his test, also worth 100 points, to average 90 points for the 5 tests given this term?
View SolutionKanaka took 8 tests for her social studies class. Each test has a maximum score of 100 and a minimum score of 0. On the 8 tests, Kanaka's mean score was 90. More than a quarter of her tests have scores less than 85. IF the average of the remaining tests is x, which of the following must be true?
View SolutionBrian plans to complete a 100-mile bike race for charity. According to his registration materials, he will need to ride at an average speed of 12.5 miles per hour if he wants to complete the course before it closes. On a pratice ride the week before the race, Brain rides 60 miles and trackes his speed. For the first 30 miles, his average speed is 16 miles per hour, and for the next 30 miles, his average speed is 15 miles per hour. If Brian can match these speeds for the first 60 miles of the charity race, then he rests for that total of 1 hour after that, what approximately speed must he maintain for the last 40 miles in order to complete the ride on time?
View Solution
