Select the graph of (x−4)225+(y−9)24=1

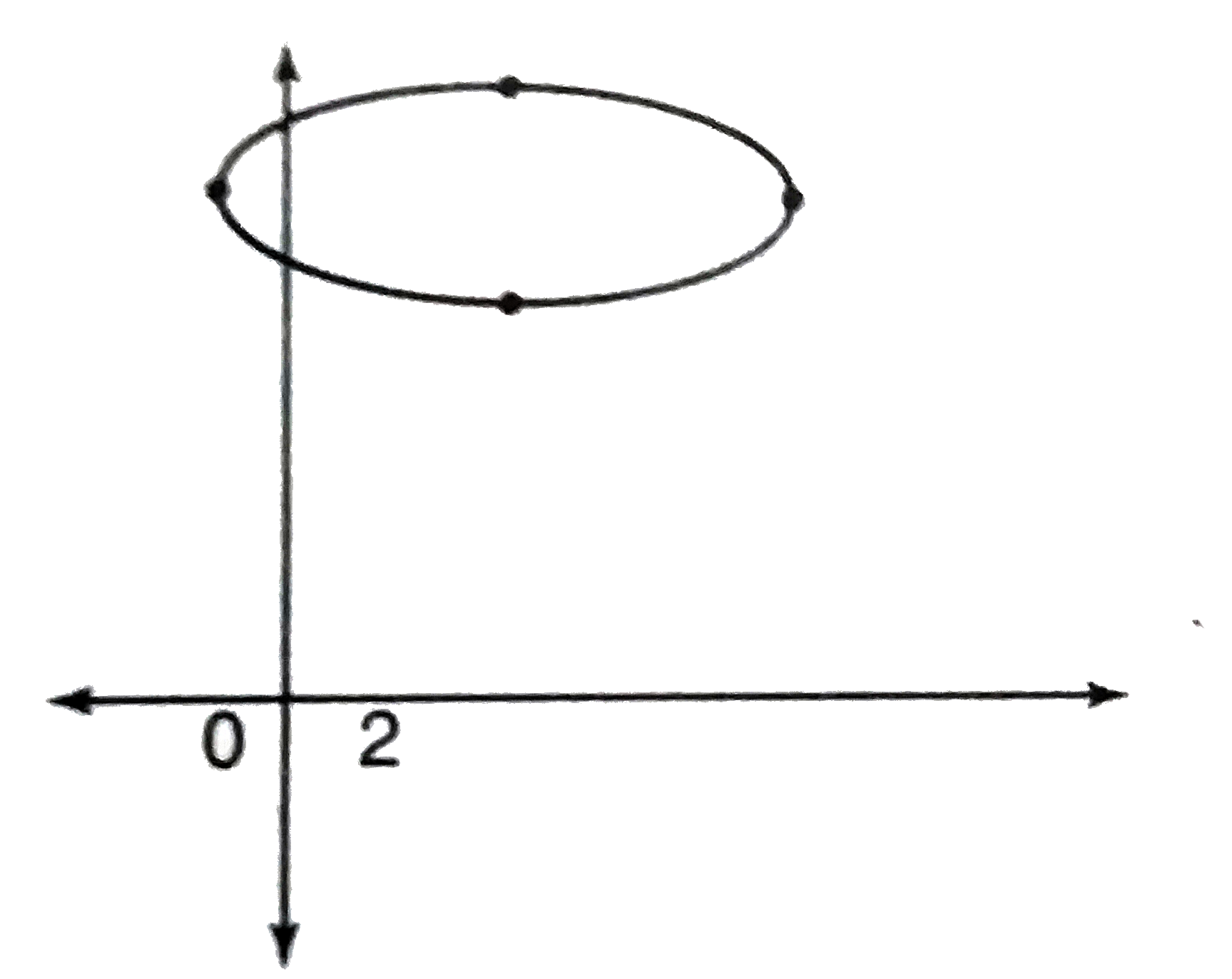
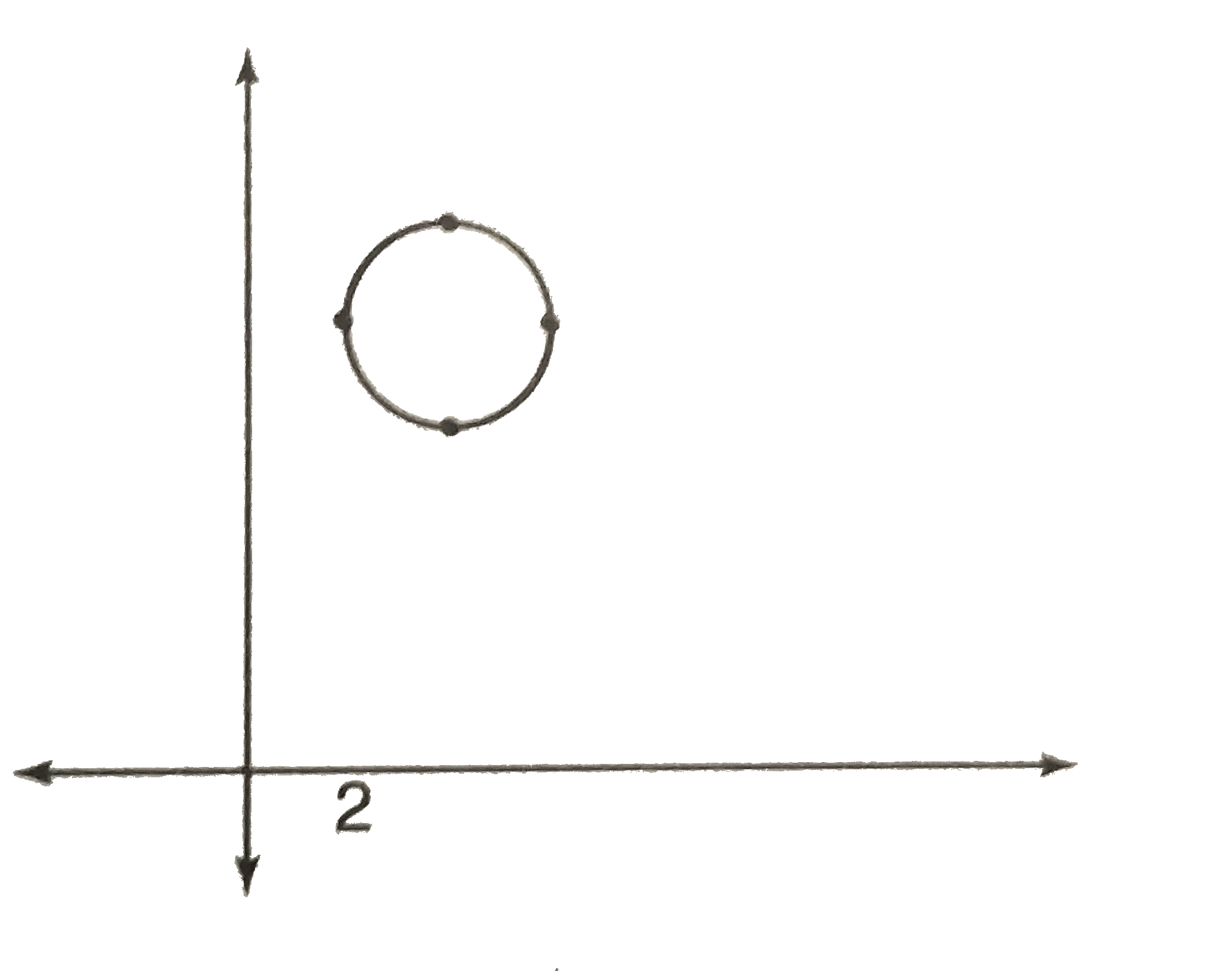
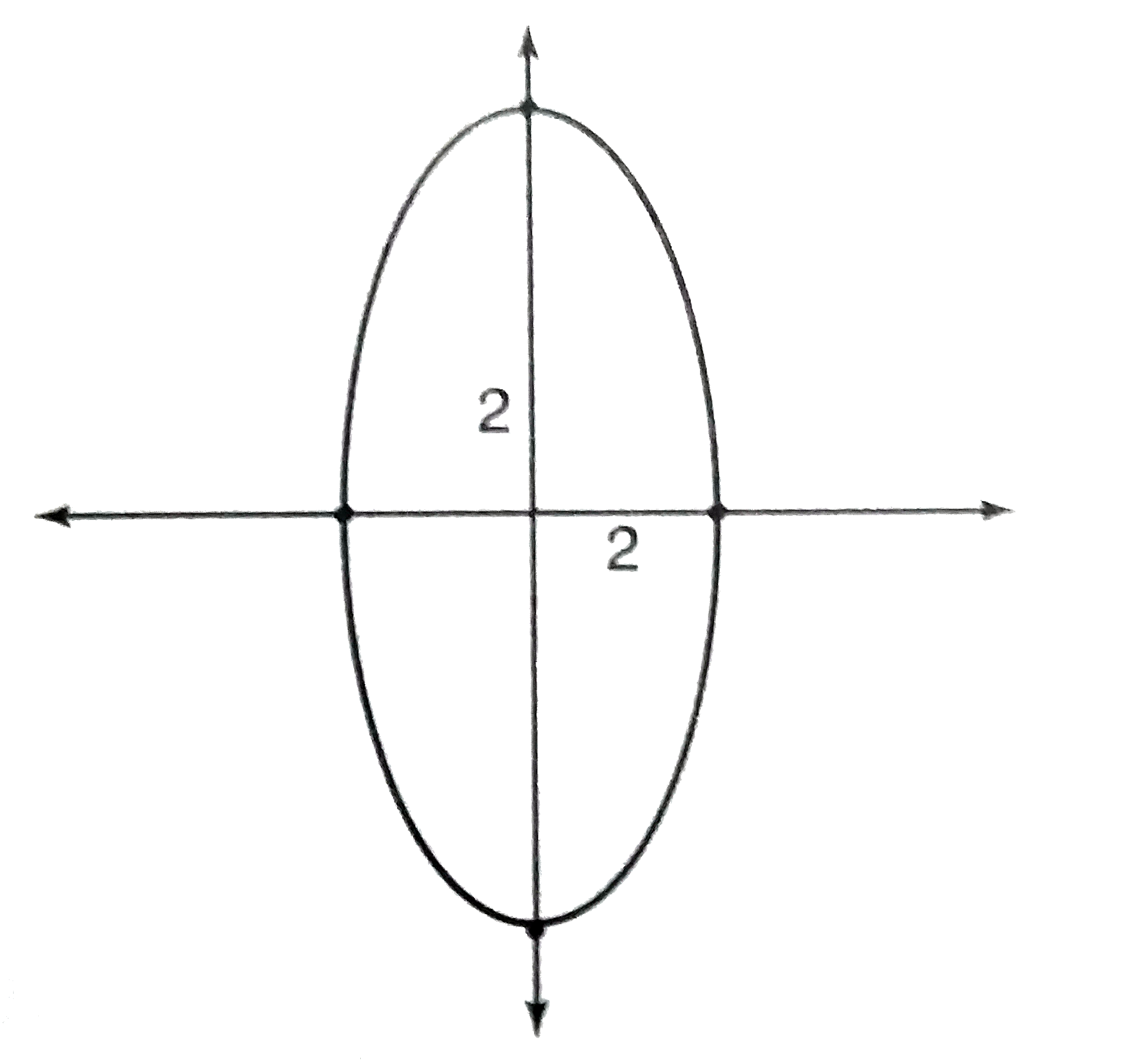
The correct Answer is:B
To solve the given problem, we will analyze the equation of the ellipse step by step and identify the correct graph representation.
Step 1: Identify the standard form of the ellipse
The given equation is:
(x−4)225+(y−9)24=1
This is in the standard form of an ellipse:
(x−h)2a2+(y−k)2b2=1
where (h,k) is the center of the ellipse, a is the semi-major axis, and b is the semi-minor axis.
Step 2: Identify the center of the ellipse
From the equation, we can see that:
- h=4
- k=9
Thus, the center of the ellipse is at the point (4,9).
Step 3: Identify the lengths of the axes
Next, we determine the lengths of the semi-major and semi-minor axes:
- a2=25⇒a=√25=5
- b2=4⇒b=√4=2
Here, a=5 is the semi-major axis and b=2 is the semi-minor axis.
Step 4: Determine the orientation of the ellipse
Since a>b, the major axis is horizontal. The lengths of the axes indicate that the ellipse stretches 5 units horizontally from the center and 2 units vertically.
Step 5: Plot the ellipse
The center of the ellipse is at (4,9), and it extends:
- Horizontally: from 4−5=−1 to 4+5=9
- Vertically: from 9−2=7 to 9+2=11
Step 6: Compare with the given options
Now, we need to compare the characteristics of the ellipse we derived with the options provided:
- The center should be at (4,9).
- The horizontal extent should be from −1 to 9.
- The vertical extent should be from 7 to 11.
Conclusion
After analyzing the options, we find that the graph that matches these characteristics is option B.
---
The given equation is:
(x−4)225+(y−9)24=1
This is in the standard form of an ellipse:
(x−h)2a2+(y−k)2b2=1
where (h,k) is the center of the ellipse, a is the semi-major axis, and b is the semi-minor axis.
From the equation, we can see that:
- h=4
- k=9
Next, we determine the lengths of the semi-major and semi-minor axes:
- a2=25⇒a=√25=5
- b2=4⇒b=√4=2
Since a>b, the major axis is horizontal. The lengths of the axes indicate that the ellipse stretches 5 units horizontally from the center and 2 units vertically.
The center of the ellipse is at (4,9), and it extends:
- Horizontally: from 4−5=−1 to 4+5=9
- Vertically: from 9−2=7 to 9+2=11
Now, we need to compare the characteristics of the ellipse we derived with the options provided:
- The center should be at (4,9).
- The horizontal extent should be from −1 to 9.
- The vertical extent should be from 7 to 11.
After analyzing the options, we find that the graph that matches these characteristics is option B.
Similar Questions
Knowledge Check
The equations of the asymptotes of the graph of 4x2−9y2=36 are
Ay=x and y=-xBy=0 and x=0Cy=23xandy=−23xDy=32xandy=−32xThe eccentricity of the ellipse x225+y29=1 is ,
Aa)45B−45C35Dd)−35
Sketch the graph : y=4cos2x
View SolutionFind the area enclosed by the graph of x2y2−9x2−25y2+225=0
View SolutionFind the area enclosed by the graph of x2y2−9x2−25y2+225=0.
View SolutionIf x,y∈R, satisfies the equation (x−4)24+y29=1 , then the difference between the largest and the smallest valus of the expression x24+y29 is_____
View SolutionThe line y=2t2 meets the ellipse x29+y24=1 in real points if
View SolutionDraw a rough sketch of the graph of the curve x24+y29=1 and evaluate the area of the region under the curve and above the x-axis.
View Solution
