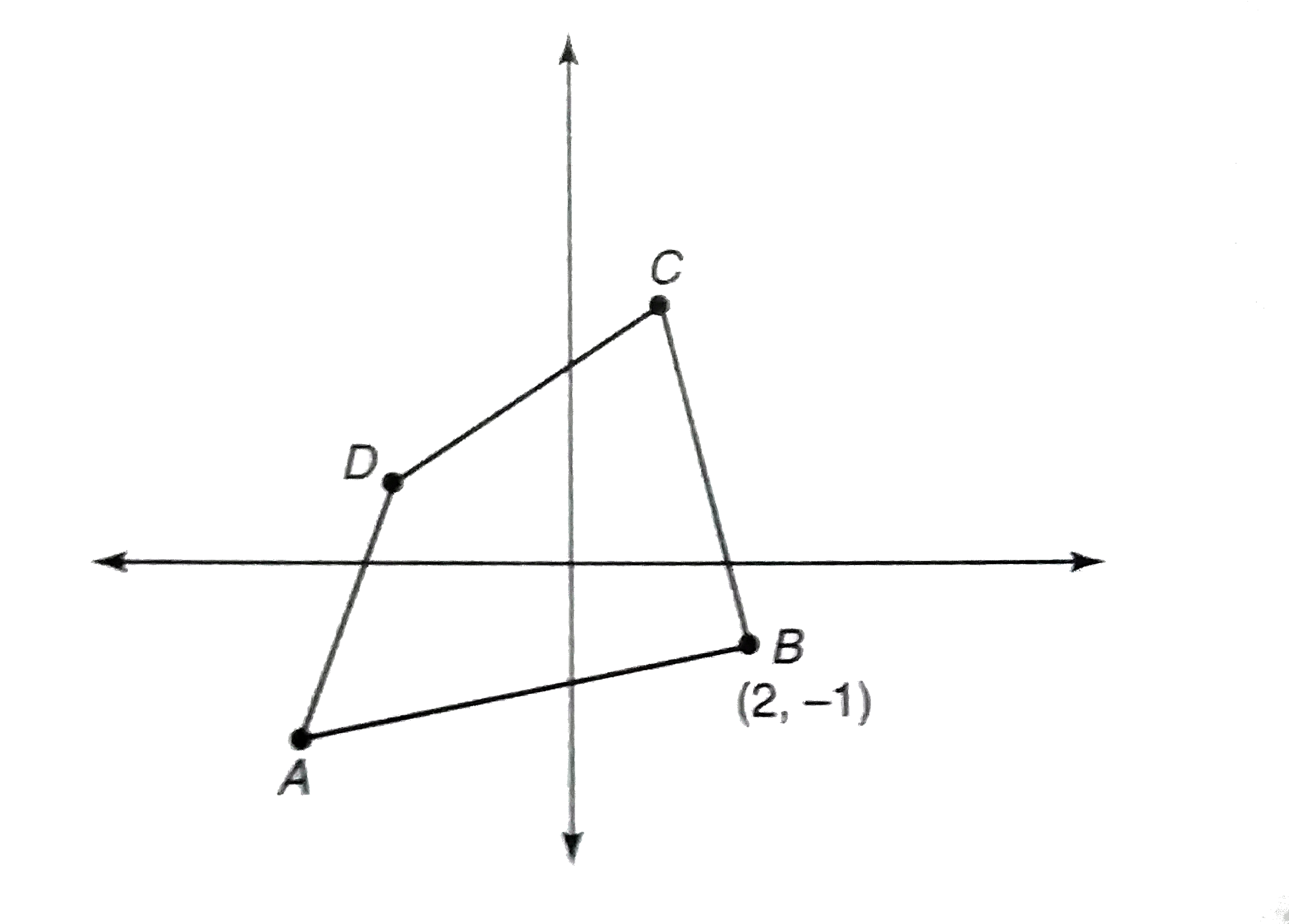
Quadrilateral ABCD has point B located at (2,-1). Find the new coodinates of B once the quadrilateral is translated (4,-7)
(4,-8)
(4,-7)
(4,6)
(6,-8)
The correct Answer is:D
Step by step video, text & image solution for Quadrilateral ABCD has point B located at (2,-1). Find the new coodinates of B once the quadrilateral is translated (4,-7) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In cyclic quadrilateral ABCD,∠A=3∠C and ∠D=5∠B. Find the measure of each angle of the quadrilateral.
View SolutionFour points A,B,C,D lie in that order on the parabola y=ax2+bx+c. The co-ordinates of A,BandD are known as A(−2,3);B(−1,1)andD(2,7). The co-ordinates of C for which the area of the quadrilateral ABCD is greatest is
View Solution
Knowledge Check
Find point B of a segment AB if A is located at (-3,7) and the midpoint of AB is located at (1,3).
A(-2,10)B(-1,5)C(3,-7)D(5,-1)
The area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThree vertices of a quadrilateral in order are (6,1)(7,2) and (−1,0). If the area of the quadrilateral is 4 sq. unit. Then the locus of the fourth vertex has the equation.
View SolutionFind the new coordinates of point (3,4) if the origin is shifted to (1, 2) by a translation.
View SolutionThe four vertices of a quadrilateral are (1, 2), (−5, 6), (7, −4) and (k, −2) taken in order. If the area of the quadrilateral is zero, find the value of k .
View SolutionA (2, 5), B (1, 0), C (-4, 3) and D (-3, 8) are the vertices of quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD. Give a special name to the quadrilateral.
View SolutionA quadrilateral has vertices (4,1),(1,7),(−6,0) AND (−1,−9). Show that mid-points of the sides of this quadrilateral form a parallelogram.
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
When the perimeter is minimum, the quadrilateral is necessarily
View Solution

