An electron beam travelling at a speed of 107 m/s strikes a metal target and absorbed by it. If the mass of the target is 0.5 g its specific heatis 100 cal /kg.∘C, find the rate at which its temperature rises. Given that the electron beam curen is 0.048 A.
The correct Answer is:65∘C/s
To solve the problem, we need to find the rate at which the temperature of the metal target rises when an electron beam strikes it. We will follow these steps:
Step 1: Calculate the energy delivered by the electron beam per second.
The energy delivered by the electron beam can be calculated using the formula:
Power(P)=Current(I)×Energy per charge(E)
Where:
- The current I=0.048A
- The energy per charge for an electron can be calculated using its kinetic energy:
E=12mv2
Where:
- m is the mass of an electron ≈9.11×10−31kg
- v=107m/s
Calculating E:
E=12×9.11×10−31×(107)2
E=12×9.11×10−31×1014
E≈4.555×10−17J
Now, we can calculate the power:
P=I×E=0.048×4.555×10−17
P≈2.18×10−18W
Step 2: Convert the power to calories per second.
1 Joule is approximately equal to 0.239 calories. Therefore, we convert the power:
P≈2.18×10−18W×0.239cal/J
P≈5.21×10−19cal/s
Step 3: Calculate the mass of the target in kg.
The mass of the target is given as 0.5 g, which we convert to kg:
m=0.5g=0.5×10−3kg=5×10−4kg
Step 4: Calculate the temperature rise using the specific heat formula.
The temperature rise can be calculated using the formula:
ΔT=Qm⋅c
Where:
- Q is the heat absorbed per second (which is the power calculated),
- m is the mass of the target,
- c is the specific heat capacity.
Given that the specific heat c=100cal/kg⋅∘C:
Now substituting the values:
ΔT=5.21×10−195×10−4×100
ΔT=5.21×10−195×10−2
ΔT≈1.042×10−17∘C/s
Final Answer
The rate at which the temperature of the metal target rises is approximately:
ΔT≈1.042×10−17∘C/s
- The current I=0.048A
- The energy per charge for an electron can be calculated using its kinetic energy:
- m is the mass of an electron ≈9.11×10−31kg
- v=107m/s
E=12×9.11×10−31×1014
E≈4.555×10−17J
P≈2.18×10−18W
P≈5.21×10−19cal/s
- Q is the heat absorbed per second (which is the power calculated),
- m is the mass of the target,
- c is the specific heat capacity.
ΔT=5.21×10−195×10−2
ΔT≈1.042×10−17∘C/s
Topper's Solved these Questions
- HEAT AND THERMAL EXPANSIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT AND THERMAL EXPANSIONExercise:ADVANCE MCQs WITH ONE OR MORE OPTIONIS CORRECT
Explore 24 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Unsolved Numerical Problems
Explore 107 Videos
- HEAT TRANSFER Book:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT TRANSFER Exercise:Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
Explore 66 Videos
Similar Questions
In an experiment with high energy beam, hydrogen ions each of 1.67×10−27 kg strike a stationary and thermally insulated target with a velocity of 2×107ms−1 at the rate of 1015 ions per second. If the mass of the target is 500 g and specific heat 0.09kcalg−1.∘C−1, find the time taken for the temperature of the target to rise by 100∘C, assuming the whole energy of the ions is converted to heat and absorbed by the target.
View SolutionA laser beam of wavelength λ1=5×10–7m strikes normally a blackened plate and produces a force of 10–5N. Mass of the plate is 10g and its specific heat capacity is 400Jkg–1K–1. At what rate will the temperature of the plate rise? Assume no heat loss to the surrounding.
View Solution
Knowledge Check
A 2 g bullet moving with a velocity of 200 m/s is brought to a sudden stoppage by an obstacle. The total heat produced goes to the bullet. If the specific heat of the bullet is 0.03cal/g∘C, the rise in its temperature will be
A158.0∘CB15.80∘CC1.58∘CD0.1580∘CA 10.0-g bullet traveling horizontally at 755 m/s strikes a stationary target and stops after penetrating 14.5 cm into the target. What is the average force of the target on the bullet ?
A1.97×104NB6.26×103NC2.07×105ND3.13×104NThe temperature of a silver bar rised by 10.0∘C when it absorbs 1.23kJ of energy by heat. The mass of bar is 525g. Determine the specific heat of silver.
A294J/kg∘CB234J/kg∘CC334J/kg∘CD394J/kg∘C
A bullet of mass 5 g travelling with a speed of 210 m/s, strikes a fixed wooden target. One half of its kinetic energy is converted into heat in the bullt while the other half is coverted into heat in the wood. The rise of temperature of the bullet if the specific heat of its meterial is 0.030 cal/(g−∘C)(1cal=4.2×107 ergs) close to :
View SolutionA 1 kg hammer with a velocity of 50ms1 strikes a 100 g iron nail driving it into a block of wood. If half of the energy of the hammer goes into heating the nail, find the rise in its temperature, given Ciron=480Jkg−1K−1
View SolutionThe anode of a diode valve ils bmbarded by a stream of electrons each of mass 9×10−31kg moving with velocity 107ms−1. If the mass of anode is 0.5g and its specific heat capacity 100 cals per kg per kelvin (J=4.2 joules cal−1) and 3×1017 electrons hit it per second, calculate the rate at which its temperature rises.
View SolutionA 25 g bullet travelling at 400 m//s passes through a thin iron wall and emerges at a speed of 250 m/s. If the bullet absorbs 50 percent of the heat generated, a. what will be the temperature rise of the bullet? B. If the ambient temperature is 20∘C will the bullet melt, and if so how much? Given that specific heat of head is 0.03cal/gm∘C and latent heat of fusion of lead is 6000 cal/kg. It is also given that melting pont of lead is 320∘C.
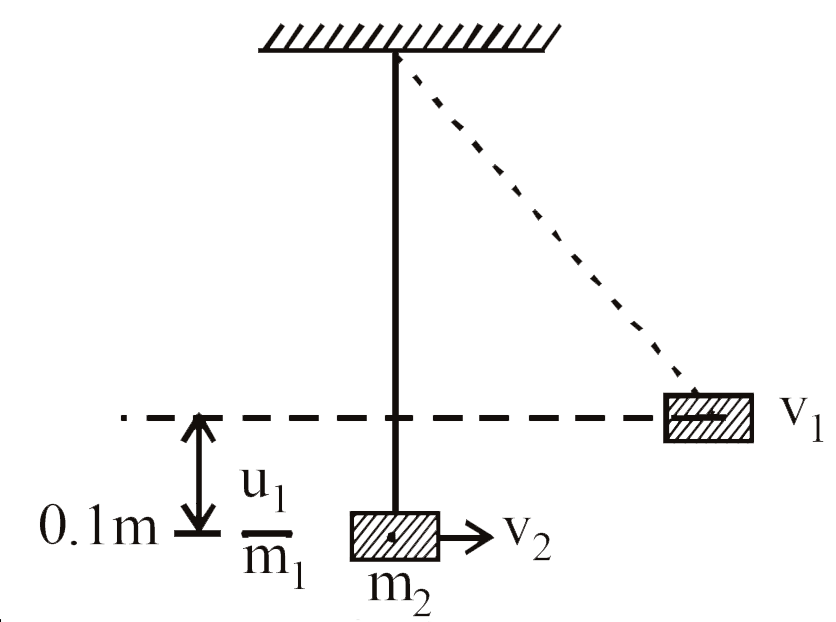
View SolutionA bullet of mass 0.01 kg travelling at a speed of 500 m/s strikes a block of mass 2 kg, which is suspended by a string of length 5 m. The centre of gravity of the block is found to rise a vertical distance of 0.1 m. The speed of the bullet after it emerges from the block will be -
View Solution