Two metal spheres (10 kg and 30 kg) moving towards each other at speeds 10 m/s and 20 m/s respectivley.They collide inelasticity. What is the rise in temperature of the combined body after collision if al the energy lost appears in the form of heat. Given that specific heat of the metal of spheres is 0.03cal/g∘C
The correct Answer is:0.65∘C
To solve the problem step by step, we will follow the principles of conservation of momentum and energy.
Step 1: Calculate the final velocity after the inelastic collision.
Given:
- Mass of sphere 1, m1=10kg
- Velocity of sphere 1, v1=10m/s
- Mass of sphere 2, m2=30kg
- Velocity of sphere 2, v2=−20m/s (negative because it is moving towards sphere 1)
Using conservation of momentum:
m1v1+m2v2=(m1+m2)V
Substituting the values:
10×10+30×(−20)=(10+30)V
100−600=40V
−500=40V
V=−50040=−12.5m/s
Step 2: Calculate the initial kinetic energy before the collision.
Using the formula for kinetic energy:
KE=12mv2
Calculating for both spheres:
KE1=12×10×(10)2=500J
KE2=12×30×(20)2=6000J
Total initial kinetic energy:
KEinitial=KE1+KE2=500+6000=6500J
Step 3: Calculate the final kinetic energy after the collision.
Using the final velocity V=−12.5m/s:
KEfinal=12(m1+m2)V2=12×40×(−12.5)2
Calculating:
KEfinal=12×40×156.25=1250J
Step 4: Calculate the energy lost in the collision.
Energy lost:
ΔKE=KEinitial−KEfinal=6500−1250=5250J
Step 5: Convert energy lost to calories.
Using the conversion factor 1cal=4.184J:
ΔKEcal=52504.184≈1257.4cal
Step 6: Calculate the rise in temperature.
Using the formula:
Q=mcΔT
Where:
- Q=1257.4cal
- m=40kg=40000g
- c=0.03cal/g∘C
Rearranging for ΔT:
ΔT=Qmc
Substituting the values:
ΔT=1257.440000×0.03=1257.41200≈1.05∘C
Final Answer:
The rise in temperature of the combined body after the collision is approximately 1.05°C.
---
- Mass of sphere 1, m1=10kg
- Velocity of sphere 1, v1=10m/s
- Mass of sphere 2, m2=30kg
- Velocity of sphere 2, v2=−20m/s (negative because it is moving towards sphere 1)
m1v1+m2v2=(m1+m2)V
Substituting the values:
10×10+30×(−20)=(10+30)V
100−600=40V
−500=40V
V=−50040=−12.5m/s
KE=12mv2
Calculating for both spheres:
KE1=12×10×(10)2=500J
KE2=12×30×(20)2=6000J
Total initial kinetic energy:
KEinitial=KE1+KE2=500+6000=6500J
KEfinal=12(m1+m2)V2=12×40×(−12.5)2
Calculating:
KEfinal=12×40×156.25=1250J
ΔKE=KEinitial−KEfinal=6500−1250=5250J
ΔKEcal=52504.184≈1257.4cal
Q=mcΔT
Where:
- Q=1257.4cal
- m=40kg=40000g
- c=0.03cal/g∘C
ΔT=Qmc
Substituting the values:
ΔT=1257.440000×0.03=1257.41200≈1.05∘C
The rise in temperature of the combined body after the collision is approximately 1.05°C.
Topper's Solved these Questions
- HEAT AND THERMAL EXPANSIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT AND THERMAL EXPANSIONExercise:ADVANCE MCQs WITH ONE OR MORE OPTIONIS CORRECT
Explore 24 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Unsolved Numerical Problems
Explore 107 Videos
- HEAT TRANSFER Book:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT TRANSFER Exercise:Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
Explore 66 Videos
Similar Questions
Two balls of masses 10 kg and 20 kg approach each other with velocities 30 m/s and 20 m/s respectively . Calculate their velocities after they undergo a perfectly eleastic collision .
View SolutionTwo lead spheres of masses 10kg and 30k approach each other with speeds 10ms−1 and 20ms−1 and collide completely inelastically. What is the heat produced by the collision? What is the rise in temperature if all the heat produced is ratained by the spheres? (Specific heat capacity of lead =31calkg−1K−1 and J=4.2 joules cal−1)
View Solution
Knowledge Check
Two bodies of masses 0.1 kg and 0.4 kg move towards each other with the velocities 1 m/s and 0.1 m/s respectively, After collision they stick together. In 10 sec the combined mass travels
A120 mB0.12 mC12 mD1.2 mTwo steel balls A and B of mass 10 kg and 10 g rolls towards each other with 5 m/s and 1 m/s respectively on a smooth floor. After collision, with what speed B moves (perfectly elastic collision)?
A8msB10msC11msDZeroTwo steel balls A and B of mass 10 kg and 10 g rolls towards each other with 5m/s and 1 m/s respectively on a smooth floor. After collision, with what speed B moves [perfectly elastic collision]?
A8 m/sB10 m/sC11 m/sDZero
Two particles A and B of equal size but of masses m kg and 2 m kg are moving directly towards each other with speeds 21 m/s and 4 m/s respectively. After collision, A moves with a speed of 1 m/s in the original direction. Then:
View SolutionA 10kg ball and a 20kg ball approach each other with velocities 20m/s and 10m/s respectively. What are their velocities after collision, if the collision is perfectly elastic ?
View SolutionFind the loss of KE of the two particles of mass m1=3kg&m2=6kg, moving towards each other with speed u1=5m/s,u2=10m/s respectively. The coefficient of restitution of collision of the particles is e = 0.5.
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then
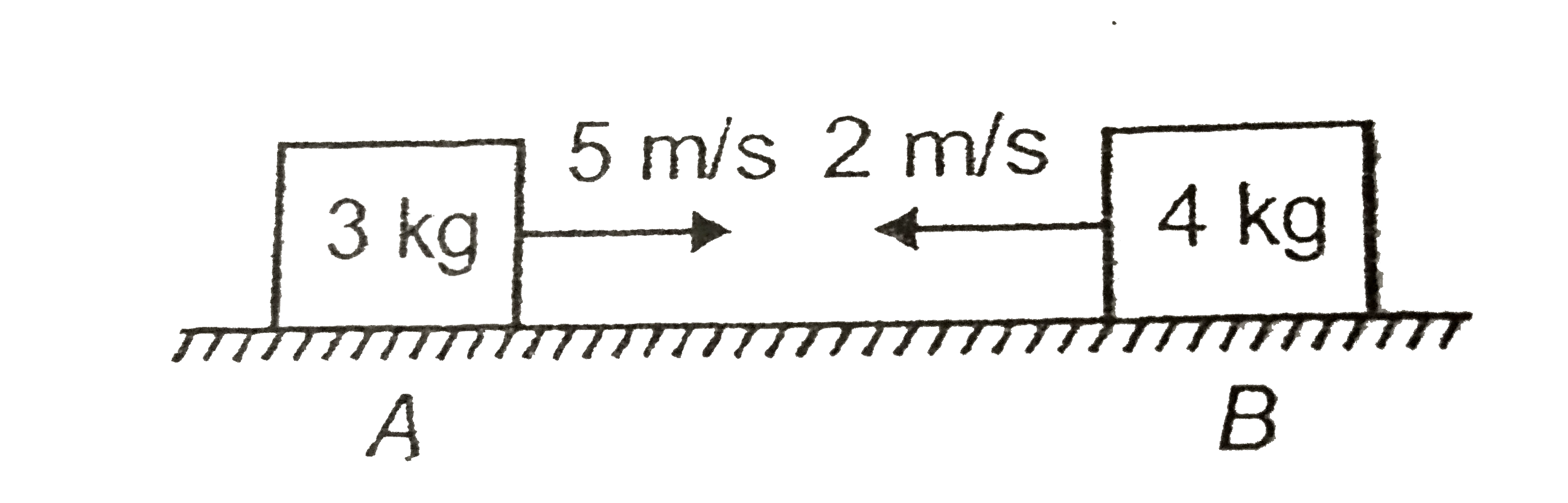
Velocity of A after collision
View SolutionA ball A of mass 3 kg and a ball B of mass 4 kg are moving alogn the same straight line with speeds of 7m/s and 5 m/s respectively. They approach each other and collide. What is the speed of B after collision, If the coefficient of restitution is 34?
View Solution