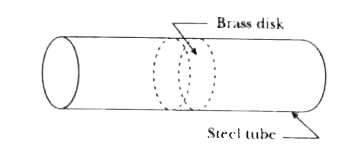
A linear accelerator consists of a hundred brass discs tightly fitted into a steel tube. At 40∘C the diameter of each disc is 10.02 cm. The system is assembled by cooling the discs in dry ice at −60∘C to enable them to slide into the close fitting tube. if the coefficient of linear expansion of brass is 2×10−5.∘C−1, the diameter of each disc in dry ice will be
9.94 cm
9.96 cm
9.98 cm
10.00 cm
To solve the problem, we need to determine the diameter of each brass disc when cooled to −60°C. We will use the formula for linear expansion to find the change in diameter due to the temperature change.
1. Identify Initial Conditions:
- Initial diameter of each disc at 40°C, \( D_i = 10.02 \, \text{cm} \)
- Final temperature, \( T_f = -60°C \)
- Initial temperature, \( T_i = 40°C \)
- Coefficient of linear expansion of brass, \( \alpha = 2 \times 10^{-5} \, °C^{-1} \)
2. Calculate the Change in Temperature:
\(
\Delta T = T_f - T_i = -60°C - 40°C = -100°C
\)
3. Use the Linear Expansion Formula:
The change in diameter due to temperature change can be calculated using the formula:
\(
\Delta D = D_i \cdot \alpha \cdot \Delta T
\)
Substituting the known values:
\(
\Delta D = 10.02 \, \text{cm} \cdot (2 \times 10^{-5} \, °C^{-1}) \cdot (-100°C)
\)
4. Calculate the Change in Diameter:
\(
\Delta D = 10.02 \cdot 2 \times 10^{-5} \cdot (-100) = 10.02 \cdot (-0.002) = -0.02004 \, \text{cm}
\)
5. Calculate the Final Diameter:
The final diameter \( D_f \) at −60°C can be calculated as:
\(
D_f = D_i + \Delta D
\)
Substituting the values:
\(
D_f = 10.02 \, \text{cm} - 0.02004 \, \text{cm} = 10.02 - 0.02004 = 9.99996 \, \text{cm}
\)
6. Round the Final Diameter:
Rounding to a reasonable number of significant figures, we get:
\(
D_f \approx 10.00 \, \text{cm}
\)
Final Answer:
The diameter of each disc in dry ice at −60°C will be approximately 10.00 cm.
---
- Initial diameter of each disc at 40°C, \( D_i = 10.02 \, \text{cm} \)
- Final temperature, \( T_f = -60°C \)
- Initial temperature, \( T_i = 40°C \)
- Coefficient of linear expansion of brass, \( \alpha = 2 \times 10^{-5} \, °C^{-1} \)
\(
\Delta T = T_f - T_i = -60°C - 40°C = -100°C
\)
The change in diameter due to temperature change can be calculated using the formula:
\(
\Delta D = D_i \cdot \alpha \cdot \Delta T
\)
Substituting the known values:
\(
\Delta D = 10.02 \, \text{cm} \cdot (2 \times 10^{-5} \, °C^{-1}) \cdot (-100°C)
\)
\(
\Delta D = 10.02 \cdot 2 \times 10^{-5} \cdot (-100) = 10.02 \cdot (-0.002) = -0.02004 \, \text{cm}
\)
The final diameter \( D_f \) at −60°C can be calculated as:
\(
D_f = D_i + \Delta D
\)
Substituting the values:
\(
D_f = 10.02 \, \text{cm} - 0.02004 \, \text{cm} = 10.02 - 0.02004 = 9.99996 \, \text{cm}
\)
Rounding to a reasonable number of significant figures, we get:
\(
D_f \approx 10.00 \, \text{cm}
\)
The diameter of each disc in dry ice at −60°C will be approximately 10.00 cm.
Topper's Solved these Questions
- HEAT AND THERMAL EXPANSIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT AND THERMAL EXPANSIONExercise:ADVANCE MCQs WITH ONE OR MORE OPTIONIS CORRECT
Explore 24 Videos
- HEAT AND THERMAL EXPANSIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT AND THERMAL EXPANSIONExercise:UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
Explore 82 Videos
- HEAT AND THERMAL EXPANSIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT AND THERMAL EXPANSIONExercise:CONCEPTUAL MCQs SINGLE OPTION CORRECT
Explore 15 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Unsolved Numerical Problems
Explore 107 Videos
- HEAT TRANSFER Book:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT TRANSFER Exercise:Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
Explore 66 Videos
Similar Questions
The given figure shows a brass disk tightly filled into a steel tube. The coefficient of linear expansion of the brass is 2.00×10−5 per ∘C . The system was assembled by cooling the disks in dry ice (−57∘C) to enable them to just slide into the close-fitting tube. If the diameter of a disk is 80.00 mm at 43∘C , what is its diameter in the dry ice?
View SolutionA brass disc has a hole of diameter 2.5 cm at 27∘C. Find the change in the diameter of the hole of the disc when heated to 327∘C. Given coefficient of linear expansion of brass = 1.9×10−5.∘C−1
View Solution
Knowledge Check
The length of a brass rod is 1.5 m. Its coefficient of linear expansion is 19×10−6K−1 Find the increase in length of the rod if it is heated through 20∘C.
A3.6×10−6mB5.7×10−6mC5.7×10−4mD3.6×10−4mWhen the temperature of a coin is raised by 75∘C , the coin's diameter increase by 2.3×10−5m . If the original diameter of the coin is 1.8×10−2 m, find the coefficient of linear expansion .
A5.4×10−5/∘CB1.7×10−5/∘CC9.8×10−6/∘CD3.1×10−6/∘C
A sheet of brass is 50 cm long and 10 cm broad at 0∘C. The area of the surface increases by 1.9cm2 at 100∘C. Find the coefficient of linear expansion of bras.
View SolutionBy how much amount should the temperature of a steel rod be increased so that its length increases by 0.5%? The coefficient of linear expansion of steel is 1.2×10−5C−1
View SolutionA circular hole is made on a copper disc. The diameter of this hole is 10 cm at 27∘C . If disc is heated upto 227∘C than calculated the change in diamter of hole . (Given coefficient of linear expansion of copper is 1.7×10−5∘C−1)
View SolutionA brass scale is graduated at 10∘C. What is the true length of a zinc rod which measures 60.00 cm on this scale at 30∘C?
Coefficient of linear expansion of brass=18×10−6K−1.
View SolutionAn iron plug is to be placed in a ring made of brass. At room temperature 28∘C the diameter of the plug is 9.114 cm and that of the inside of the ring is 9.097 cm. To what common temperatue these both be brought in order to fit? Give that coefficient of linear expansion of iron is 1.1×10−5.∘C−1 and that of brass sis 1.9×10−5.∘C−1
View SolutionA blacksmith fixes iron ring on the rim of the wooden wheel of a bullock cart. The diameter of the rim and the ring are 5.243m and 5.231m respectively at 27∘C. To what temperature should the ring be heated so as to fit the rim of the wheel ? Coefficient of linear expansion of iron =1.20×10−5K−1
View Solution

