The Pyrex glass is having very low coefficient of linear expansion. It is also used as a very good transparent heat resistor as compared to ordinary glass. Explain?
To explain why Pyrex glass, which has a very low coefficient of linear expansion, is used as a good transparent heat resistor compared to ordinary glass, we can break down the reasoning into several steps:
1. Understanding Coefficient of Linear Expansion:
- The coefficient of linear expansion (α) is a measure of how much a material expands per unit length for a unit change in temperature. A low α means that the material will not expand significantly when heated.
2. Properties of Pyrex Glass:
- Pyrex glass has a low coefficient of linear expansion compared to ordinary glass. This means that when Pyrex is subjected to temperature changes, its dimensions (length, area) change very little.
3. Importance of Dimensional Stability in Resistors:
- In applications where resistors are used, it is crucial that their resistance does not fluctuate with temperature. The resistance (R) of a material is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
4. Effect of Temperature on Resistance:
- When the temperature of a resistor increases, its dimensions can change due to thermal expansion. If the length (L) increases significantly due to a high α, the resistance will also change, which is undesirable in many applications.
5. Minimizing Changes in Dimensions:
- To keep the resistance value stable, we need to minimize the changes in length (ΔL) and area (ΔA) with temperature. The change in length due to temperature change can be expressed as:
ΔL=L0αΔT
where L0 is the original length and ΔT is the change in temperature.
6. Choosing Materials with Low α:
- Since we want to minimize ΔL, we should choose materials with a low coefficient of linear expansion. Pyrex glass, having a low α, is ideal for this purpose because it will experience minimal dimensional changes when subjected to temperature variations.
7. Conclusion:
- Therefore, Pyrex glass is preferred for making transparent heat resistors because it maintains its dimensions better than ordinary glass when exposed to heat, ensuring that the resistance remains stable and reliable.
- The coefficient of linear expansion (α) is a measure of how much a material expands per unit length for a unit change in temperature. A low α means that the material will not expand significantly when heated.
- Pyrex glass has a low coefficient of linear expansion compared to ordinary glass. This means that when Pyrex is subjected to temperature changes, its dimensions (length, area) change very little.
- In applications where resistors are used, it is crucial that their resistance does not fluctuate with temperature. The resistance (R) of a material is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
- When the temperature of a resistor increases, its dimensions can change due to thermal expansion. If the length (L) increases significantly due to a high α, the resistance will also change, which is undesirable in many applications.
- To keep the resistance value stable, we need to minimize the changes in length (ΔL) and area (ΔA) with temperature. The change in length due to temperature change can be expressed as:
ΔL=L0αΔT
where L0 is the original length and ΔT is the change in temperature.
- Since we want to minimize ΔL, we should choose materials with a low coefficient of linear expansion. Pyrex glass, having a low α, is ideal for this purpose because it will experience minimal dimensional changes when subjected to temperature variations.
- Therefore, Pyrex glass is preferred for making transparent heat resistors because it maintains its dimensions better than ordinary glass when exposed to heat, ensuring that the resistance remains stable and reliable.
Topper's Solved these Questions
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - CONCEPTUAL MCQs SINGLE OPTION CORRECT
15 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - NUMERICAL MCQs SINGLE OPTIONS CORRECT
81 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - PRACTICE EXERCISE
40 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems
107 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
66 Videos
Similar Questions
A liquid having coefficient of volume expansion γ0 is filled in a cylindrical glass vessel. Glass has a coefficient of linear expansion of αg. The liquid along with the container is heated to raise their temperature by ΔT. Mass of the container is negligible. (a) find relationship between αg and γ0 if it was found that the centre of mass of the system did not move due to heating.
(b) Find relationship between αg and γ0 if the fraction of volume of the container occupeid by the liquid does not change due to heating.
View SolutionA liquid having a coefficient of volume expansion γ is filled in a cylindrical vessel made out of glass having coefficient of lienar expansion α=γ5 . At room temperature , the level of liquid in the vessel isl0 and when the temperature is increased by ΔT, the level of liquid in the vessel becomes l≈l0=(1+nαΔT). What is the value of n ? [Given,αΔT<<1]
View Solution
Knowledge Check
A metal rof having coefficient of linear expansion α and Young's modulus Y is heated to raise its temperature by Δθ. The stress exerted by the rod is
AYαΔθBYΔθαCYαΔθDαΔθYA metal rod having coefficient of linear expansion (α) and Young's modulus (Y) is heated to raise the temperature by Δθ. The stress exerted by the rod
AYαΔθBYΔθαCYαΔθDαΔθYIn a mercury-glass thermometer the cross-section of the capillary portion is A0 and the volume of the bulb is V0 at 273K. If α and γ are the coefficients of linear and cubical expansion coefficients of glass and mercury respectively then length of mercury in the capillary at temperature t∘C is (Ignore the increase in cross-sectional area of capillary)
_E01_142_Q01.png) AV0A0(γ−3α)tBV0A0(2γ−3α)tCV0A0(γ−3α)(t+273)DV0γtA0
AV0A0(γ−3α)tBV0A0(2γ−3α)tCV0A0(γ−3α)(t+273)DV0γtA0
The real coefficient of volume expansion of glycerine is 0.000597 per .∘C. Then the apparent volume coefficient of expansion of glycerine in glass will be (linear expansion of glass is 0.000009 per .∘C.)
View SolutionIn a cylidrical glass container a solid silica is placed vertically at its bottom and remaining space is filled with mercury upto the top level of the silica. The volume of silica remains unchanged with variation in temperature. The coefficient of cubical expansion of mercury is γ and coefficient of linear expansion of glass is α. If the top surface of silica and mercury level remain at the same level wiht the variation in temperature then the ratio of volume of silica tothe volume of mercury is equal:

View SolutionIn a compensated pendulum a triangular frame ABC is made using two different metals. AB of length l1 is made using a metal having coefficient of linear expansion α1. BC and AC of length l2 each have coefficient of linear expansion α2. A heavy bob is attached at C. Pendulum can oscillate about the pivot D. Find l2l1 so that distance of bob from the pivot point D does not change with change in temperature.
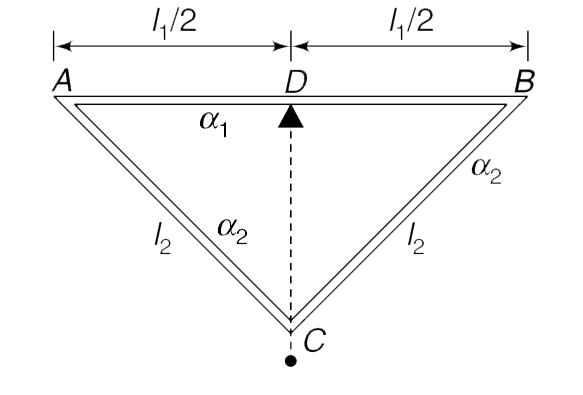
View SolutionA fluid having a thermal coefficient of volume expansion γ is filled in a cylindrical vessel up to a height h0. The coefficient of linear thermal expansion of the material of the vessel is α . If the fluid is heated with the vessel , then find the level of liquid when temperature increases by Δθ.
View SolutionWhen solid is heated , its length changes according to the relation l=l0(1+αΔT) , where l is the final length , l0 is the initial length , ΔT is the change in temperature , and α is the coefficient of linear is called super - facial expansion. the area changes according to the relation A=A0(1+βΔT), where A is the tinal area , A0 is the initial area, and β is the coefficient of areal expansion.
A metal disc having a circular hole at its center is heated . If the metal expands on heating , the diameter of the hole
View Solution
