In Figure, OABC is a squaer inscribed in a quadrant OPBQ. If OA=20cm, find the are of shaded region. [Useπ=3.14.]
Given,OA=20cm
Thus, OA=AB=20cm [Sides of a square]
∴ Using Pythagoras theorem
OB2=OA2+AB2
=(20cm)2+(20cm)2
OB=√2×(20cm)²
=20√2cm
Therefore, radius of the quadrant, r=OB=20√2cm
Area of quadrantOPBQ=90°360°×πr2
=14×3.14×(20√2cm)2
=14×3.14×400×2cm2
= 628 cm2
Area of square OABC=(side)2
=(OA)2
=(20cm)2
=400cm2
Area of the shaded region = Area of quadrant OPBQ - Area of square OABC
=628cm2−400cm2
= 228 cm2
Topper's Solved these Questions
Similar Questions
In Figure, OABC is a squaer inscribed in a quadrant OPBQ. If OA=20cm, find the are of shaded region. [Useπ=3.14.]
View Solutionfind the area of the shaded region [Use π=3.14] .
View SolutionIn the given figwe, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region (Use π = 3.14)
View SolutionIn the given figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 15 cm, find the area of the shaded region. (Use π = 3.14)

View SolutionIn the figure , a square OABC is inscribed in a quadrant OPBQ . If OA =20 cm , find the area of the shaded region.
View SolutionIn Fig. 12.31, a square OABC is inscribed in a quadrant OPBQ. If OA=20cm, find the area of the shaded region. (Use π=3.14)
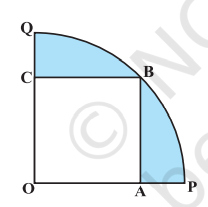
View SolutionIn the given figure, a square OABC has been inscribed in the quadrant OPBQ .If OA=20cm then the area of the shaded region is [take π=3.14]
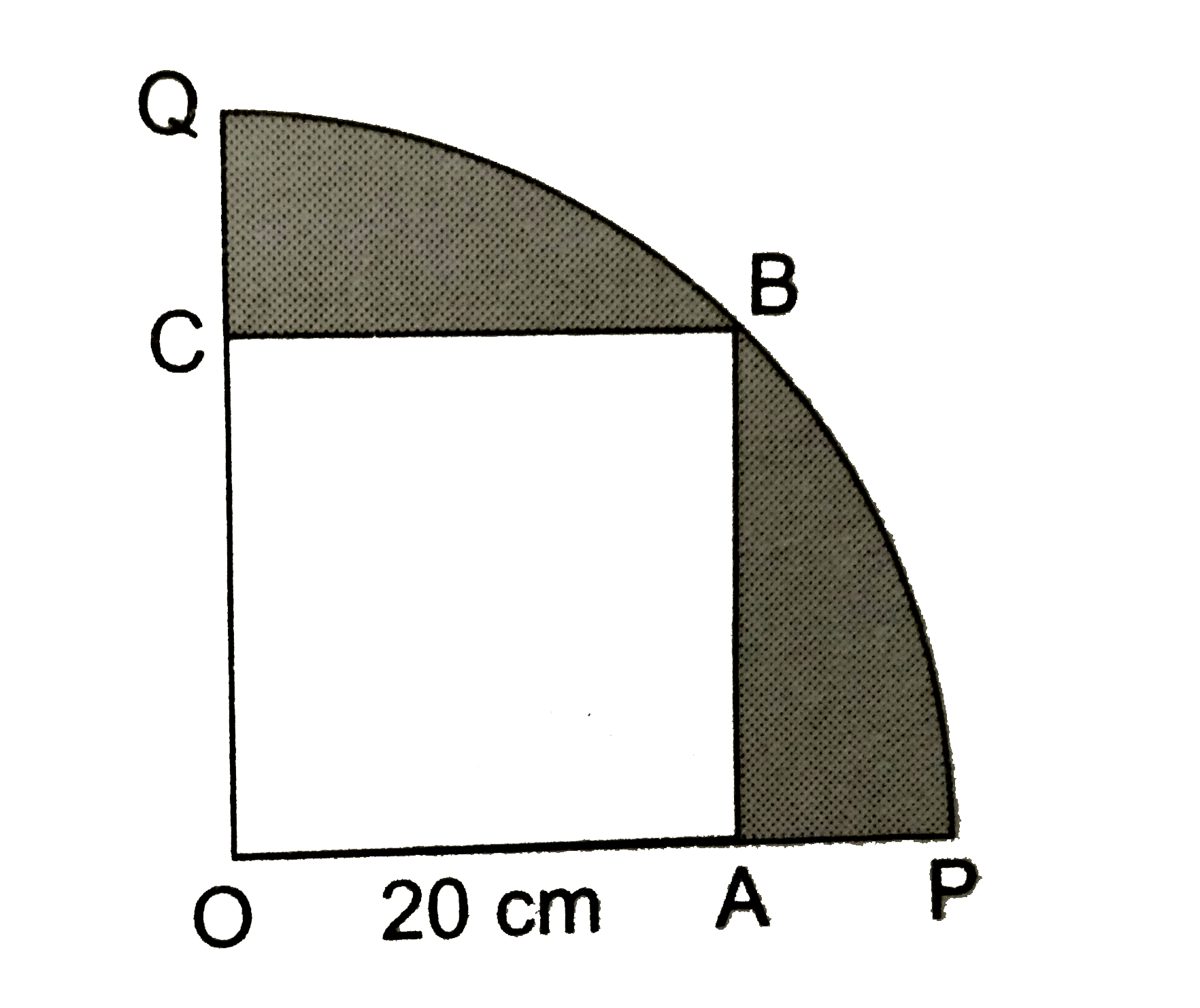
View SolutionIn the given figure square OABC is inscribed in a sector OPBQ. If OC = 20 cm, find the area of the shaded region (Use π=3.14)

View SolutionIn figure, find the area of the shaded region [Useπ=3.14]
View SolutionIn Fig. 15.99, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA=21 cm , find the area of the shaded region. (FIGURE)
View Solution
