Let ABCD be a tetrahedron such that the edges AB,ACandAD are mutually perpendicular. Let the area of triangles ABC,ACDandADB be 3, 4 and 5sq. units, respectively. Then the area of triangle BCD is 5√2 b. 5 c. √52 d. 52
{AB},{AC},{AD} are mutually perpendicular
area of △{ABC}=|{AB}||{AC}|=6
area of △{ACD}=|{AC}||{AD}|=8
area of Δ{ADB}=|{AB}||{AD}|=10
Then the area of △{BCD}=12|{{BC}}×{{BD}}|
area =12|({{AC}}−{{AB}})×({{AD}}−{{AB}})|
area =12|{AC}×{AD}−{AC}×{AB}−{AB}×{AD}+{AB}×{AB}|
area =12|{{AC}}×{{AD}}−{{AC}}×{{AB}}−{{AB}}×{{AD}}+0|
area =12|{{AC}}×{{AD}}−{{AC}}×{{AB}}−{{AB}}×{{AD}}|
area =12|{{AC}}×{{AD}}−{{AC}}×{{AB}}−{{AB}}×{{AD}}|
area =
⎷({AC}×{AD}2)2+({AC}×{AB}2)2+({AB}×{AD}2)2
area =
⎷({areaof}Δ{ACD})2+({areaof}Δ{ABC})2+({areaof}Δ{ABD})2
area =√32+42+52
area =√9+16+25
area =√50
area =5√2
Topper's Solved these Questions
Similar Questions
Knowledge Check
A and B are isotopes. B and C are isobars. If dA,dB and dC be the densities of nuclei A, B and C respectively then
AdA>dB>dCBdA<dB<dCCdA=dB=dCDdA=dB<dC
If D,E,F are the mid-points of the sides BC,CAandAB respectively of a triangle ABC, prove by vector method that AreaofDEF=14(areaofABC).
View SolutionIn the given figure, ABCD is a rectangle with AD=4 units and AE=EB.EF is perpendicular to DB and is half of DF . If the area of the triangle DEF is 5 sq. units, then what is the area of ABCD ? 18√3 sq. units (b) 20 sq. units (c) 24 sq. units (d) 28 sq. units
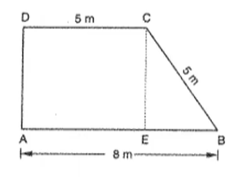
View SolutionIn quadrilateral ABCD show in Figure. ABDC and AD⊥AB. Also, AB=8m, DC=BC=5m. Find the area of the quadrilateral.
View SolutionABC is a triangle in which D is the mid-point of BC ,E andF are mid-points of DC and AE respectively. If area of ABC is 16cm2, find the area of DEF
View SolutionIn ABC,∠A=900andAD is an altitude. Complete the relation BDDA=AB() .
View SolutionIf A(1,-1,2),B(2,1,-1)C(3,-1,2) are the vertices of a triangle then the area of triangle ABC is
(A)√12 (B) √3(C) √5 (D) √13
View SolutionABCD is a cyclic quadrilateral whose diagonals ACandBD intersect at P . If AB=DC, Prove that : PAB≅PDC PA=PDandPC=PB ADBC
View Solution
