Let →u=u1ˆi+u2ˆj+u3ˆk be a unit vector in R3and→w=1√6(ˆi+ˆj+2ˆk) , Given that there exists a vector →v in R3 such that |→u×→v|=1and→w.(→u×→v)=1 which of the following statements is correct ?
There is exactly one choice for such →v
There are infinitely many choices for such →v
If ˆu lies in the xy-plane then |u1|=|u2|
If ˆu lies in the xz-plane then 2|u1|=|u3|
The correct Answer is:B, C
Step by step video, text & image solution for Let vecu = u_(1)hati + u_(2)hatj +u_(3)hatk be a unit vector in R^(3) and vecw = 1/sqrt6 ( hati + hatj + 2hatk) , Given that there exists a vector vecv " in " R^(3) such that | vecu xx vecv| =1 and vecw . ( vecu xx vecv) =1 which of the following statements is correct ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Let →u=u1ˆi+u2ˆj be a unit vector in xy plane and →w=1√6(ˆi+ˆj+2ˆk) . Given that there exists a vector →c " in " R3 " such that |→u×→v|=1 and →w. (→u×→v)=1 , then
A|u1|=|u2|B|u2|=2|u2|C2|u1|=|u2|D|u1|−3|u2|Let →u=u1ˆi+u3ˆk be a unit vector in xz-plane and →q=1√6(ˆi+ˆj+2ˆk). If there exists a vector →v in such that |→u×→u|=1and→w.(→u×→c) .Then
A|u1|=|u3|B|u1|=2|u3|C|u1|=2|u3|D2|u1|=|u3|Let →u=2ˆi−ˆj+ˆk,→v=−3ˆj+2ˆk be vectors in R3 and →w be a unit vector in the xy-plane. Then the maximum possible value of |(→u×→v).→w| is-
A√5B√12C√13D√17
The figure given below shows the orientation of two vectors →uand→v in the xy plane .
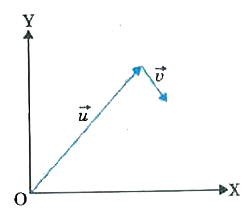
if →u=aˆi+bˆjand→v=pˆi+qˆj
Which of the following is correct ?
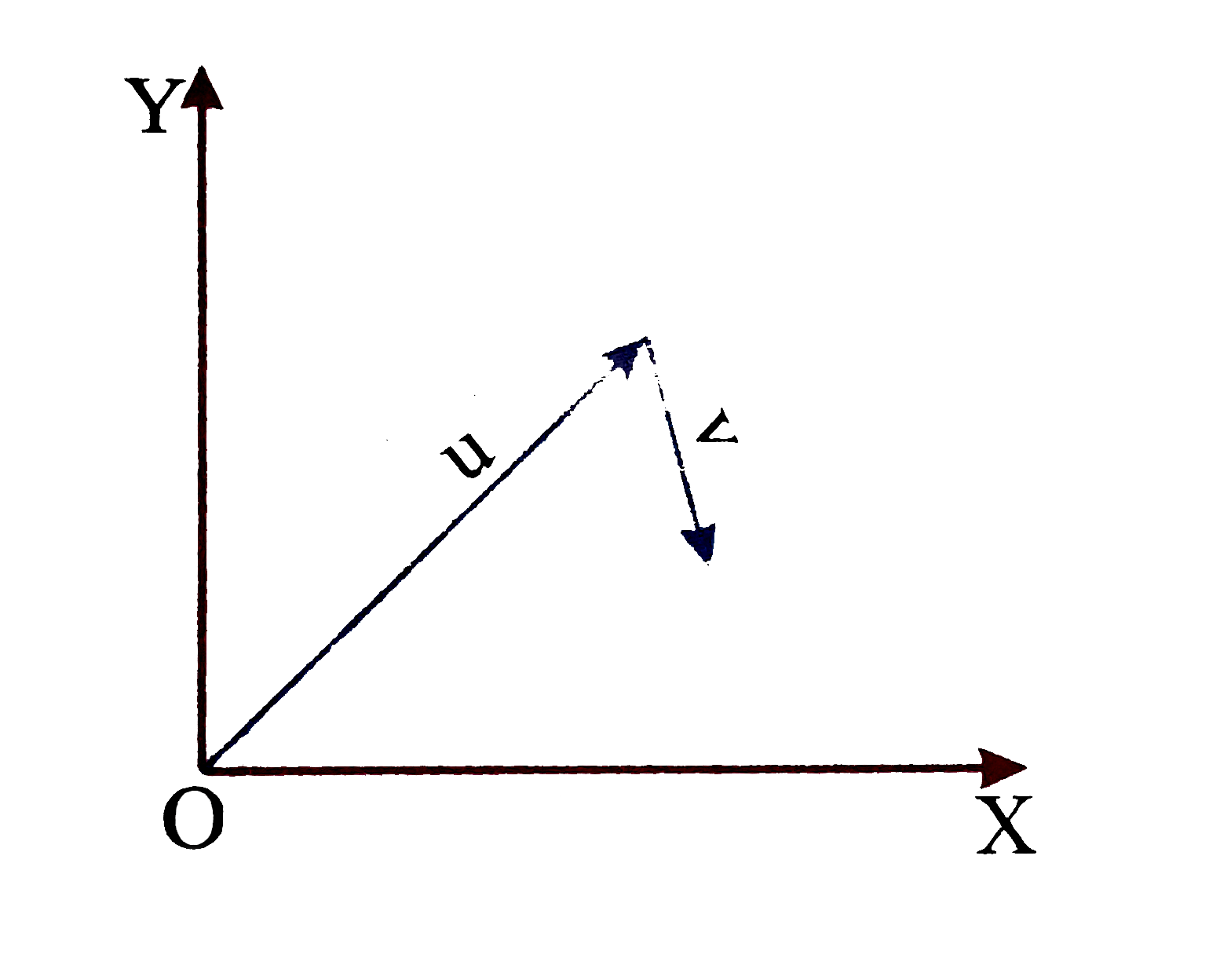
View SolutionFigure shows the orientation of two vectors u and vin the XY plane.
if→u=aˆi+bˆj and →v=pˆi+qˆj
which of the following is correct?
View SolutionThe unit vector parallel to the resultant vector of 2ˆi+4ˆj−5ˆkandˆi+2ˆj+3ˆk is
View SolutionFor three vectors, →u,→vand→w which of the following expressions is not equal to any of the remaining three ?
View SolutionLet →u=ˆi+ˆj,→v=ˆi−ˆjaandˆi−ˆjand→w=ˆi+2ˆj+3ˆk If ˆn isa unit vector such that →u.ˆn=0and→n.ˆn=0, then |→w.ˆn| is equal to
View Solution
