ABC is triangle, right angled at A. The resultant of the forces acting along −−→AB.−−→AC with magnitudes 1AB and respectively is the force along −−→AD, where D is the foot of the perpendicular from A onto BC. The magnitude of the resultant is-
(AB)(AC)AB+AC
1AB+1AC
1AD
AB2+AC2(AB)2(AC)2
The correct Answer is:C
Step by step video & text solution for ABC is triangle, right angled at A. The resultant of the forces acting along vec(AB). vec(AC) with magnitudes 1/(AB) and respectively is the force along vec(AD), where D is the foot of the perpendicular from A onto BC. The magnitude of the resultant is- by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
ABC is isosceles triangle, right angled at A. The resultant of the forces acting along −−→AB,−−→AC with magnitudes 1AB and 1AC respectively is the force along −−→AD, where D is the foot of the perpendicular from A on BC. The magnitude of the resultant is:
A(AB)(AC)AB+ACB1AB+1ACC1ADDAB2+AC2(AB)2(AC)2If −−→AB=→band−−→AC=→c then the length of the perpendicular from A to the line BC is
A∣∣→b×→c∣∣∣∣→b+→c∣∣B∣∣→b×→c∣∣∣∣→b−→c∣∣C∣∣→b×→c∣∣2∣∣→b−→c∣∣D∣∣→b×→c∣∣2∣∣→b+→c∣∣ABC is an isosceles triangle right angled at A. forces of magnitude 2√2,5and6 act along BC, CA and AB respectively. The magnitude of their resultant force is
A4B5C11+2√2D30
In a right angled triangle ABC,D is the foot of the perpendicular from B on the hypotenuse AC. If AB=3cm and BC=4cm, what is the area of △ABD
View SolutionIn a right-angled triangle ABC ,D is the foot of the perpendicular from B on the hypotenuse AC . If AB=3cm and BC=4cm, what is the area of △ABD?
View SolutionThe resultant of two forces sec B and C along sides AB , AC of triangle ABC is a force acting along AD when D is
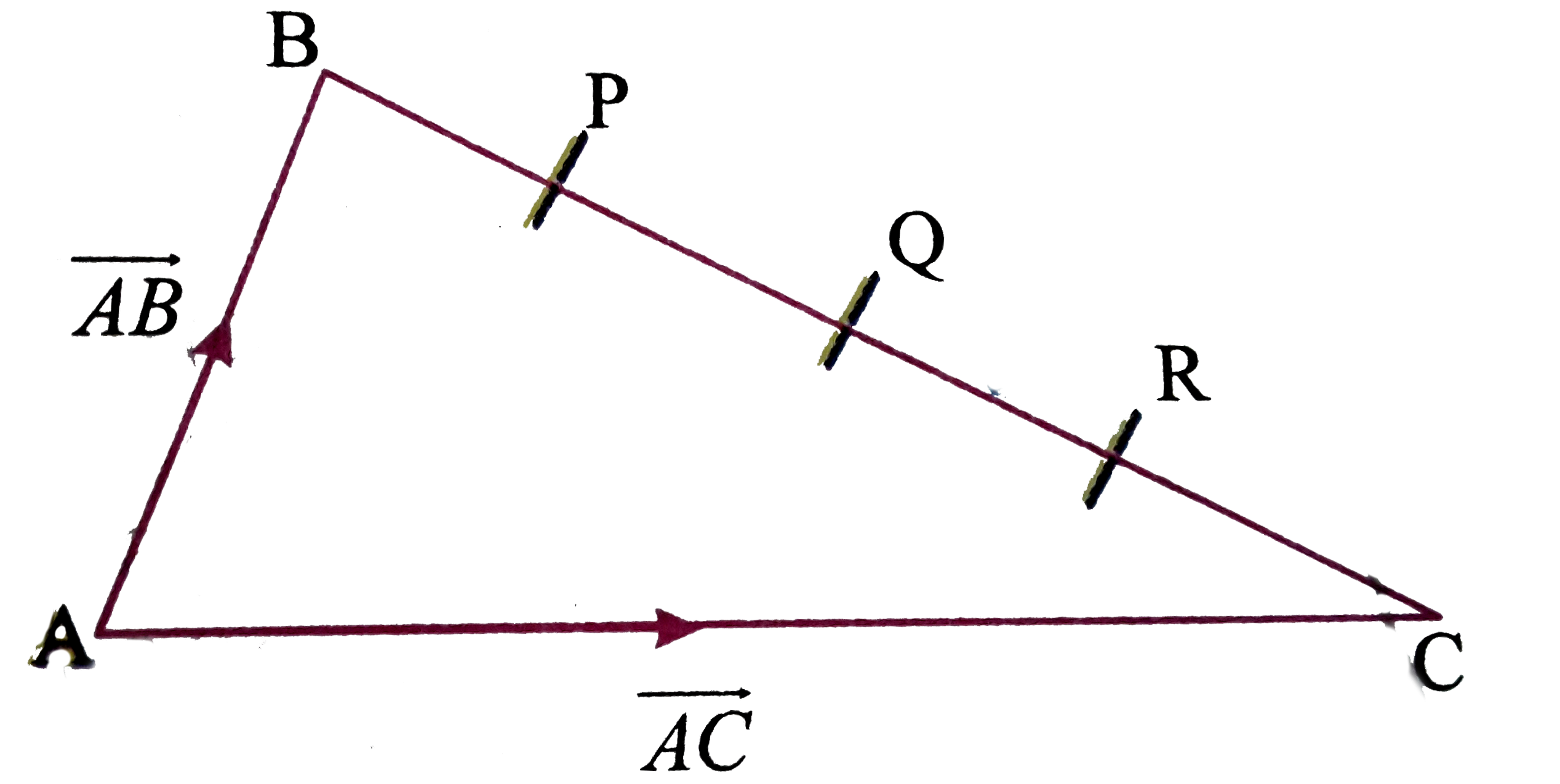
View SolutionBC is divided into four equal parts by P,Q and R.The resultant of −−→AB and 3−−→AC is
View SolutionThe resultant of two vectors →P and →Q is →R. If the magnitude of →Q is doubled, the new resultant vector becomes perpendicular to →P. Then, the magnitude of →R is equal to
View Solution
