Consider a tetrahedron with faces f1,f2,f3,f4. Let →a1,→a2,→a3,→a4 be the vectors whose magnitudes arerespectively equal to the areas of f1,f2,f3,f4 and whose directions are perpendicular to these faces in theoutward direction. Then
→a1+→a2+→a3+→a4=0
→a1+→a3=→a2+→a4
→a1+→a2=→a3+→a4
none of these
The correct Answer is:A
Step by step video, text & image solution for Consider a tetrahedron with faces f_1, f_2, f_3, f_4. Let vec a_1, vec a_2, vec a_3, vec a_4 be the vectors whose magnitudes arerespectively equal to the areas of f_1,f_2,f_3,f_4 and whose directions are perpendicular to these faces in theoutward direction. Then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTOR Book:MOTIONChapter:VECTOR Exercise:EXERCISE - 2 ( LEVEL -II)
Explore 15 Videos
- VECTOR Book:MOTIONChapter:VECTOR Exercise:EXERCISE - 3
Explore 38 Videos
- VECTOR Book:MOTIONChapter:VECTOR Exercise:EXERCISE - 1
Explore 42 Videos
- TRIGONOMETRIC EQUATIONBook:MOTIONChapter:TRIGONOMETRIC EQUATIONExercise:EXERCISE 4
Explore 10 Videos
Similar Questions
Knowledge Check
Consider a tetrahedron with faces F1,F2,F3,F4. Let →V1,→V2,→V3,→V4 be the vectors whose magnitude are respectively equal to areas of F1.F2.F3.F4 and whose directions are perpendicular to their faces in outward direction. Then ∣∣→V1+→V2+→V3+→V4∣∣, equals:
A1B4C0DNone of theseConsider a tetrahedron with faces F1,F2,F3,F4. Let →V1,→V2,→V3,→V4 be the vectors whose magnitude are respectively equal to areas of F1.F2.F3.F4 and whose directions are perpendicular to their faces in outward direction. Then ∣∣→V1+→V2+→V3+→V4∣∣, equals:
A1B4C0DNone of theseSix vector →a through →f have the magnitudes and direction indicated in the figure. Which of the following statements is true?
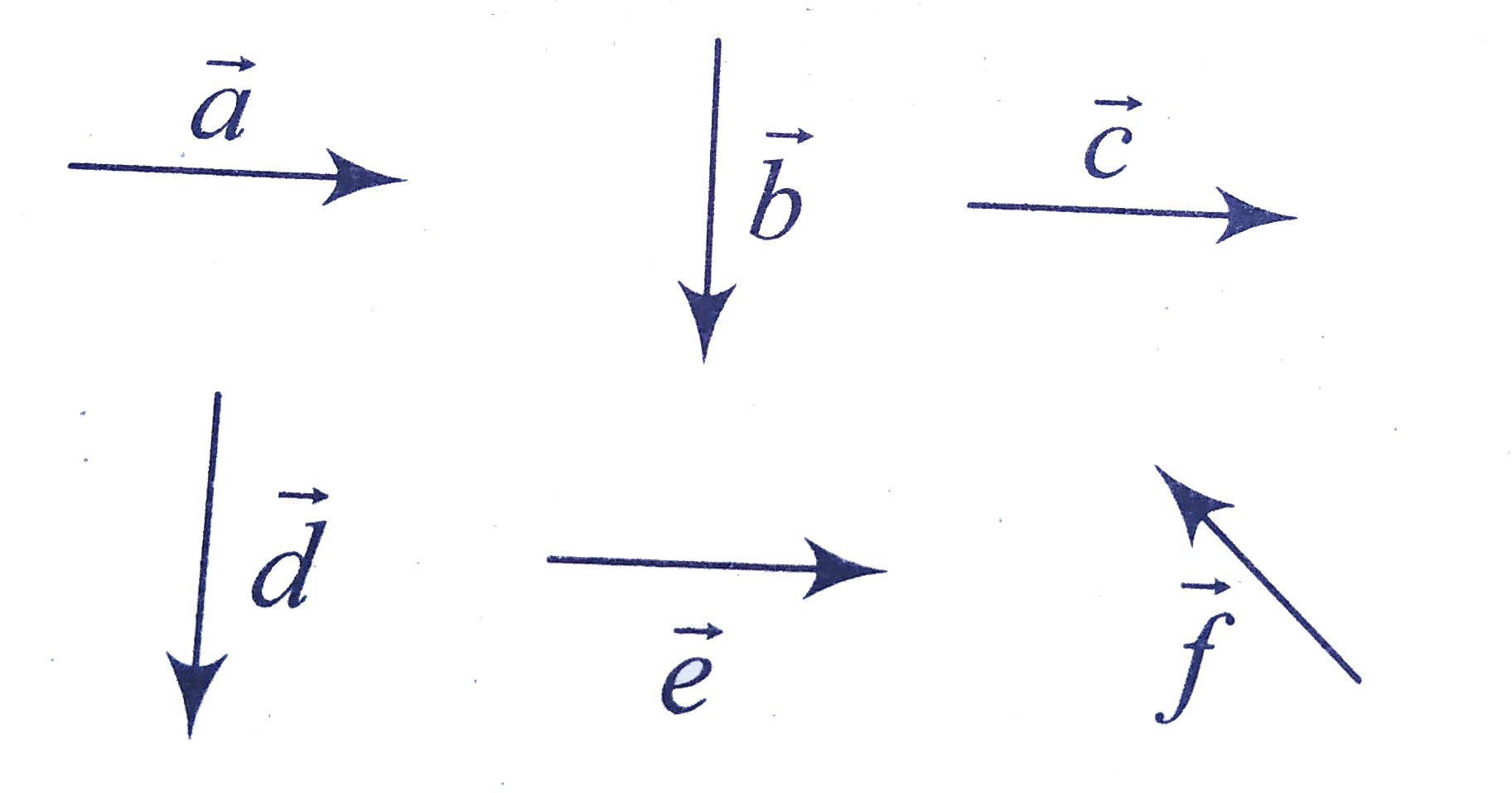 A→b+→e=→fB→b+→c=→fC→d+→c=→fD→d+→e=→f
A→b+→e=→fB→b+→c=→fC→d+→c=→fD→d+→e=→f
Find a vector →F of magnitude 50N parallel to −4ˆi+3ˆj.
View SolutionIn a four-dimensional space where unit vectors along the axes are ˆi,ˆj,ˆkandˆl,and→a1,→a2,→a3,→a4 are four non-zero vectors such that no vector can be expressed as a linear combination of others and (λ−1)(→a1−→a2)+μ(→a2+→a3)+γ(→a3+→a4−2→a2)+→a3+δ→a4=0, then a. λ=1 b. μ=−2/3 c. γ=2/3 d. δ=1/3
View SolutionConsider a vector →F=4ˆi−3ˆj. Another vector that is perpendicular to →F is
View SolutionThree forces →F1,→F2 and →F3 are represented as shown. Each of them is equal magnitude.
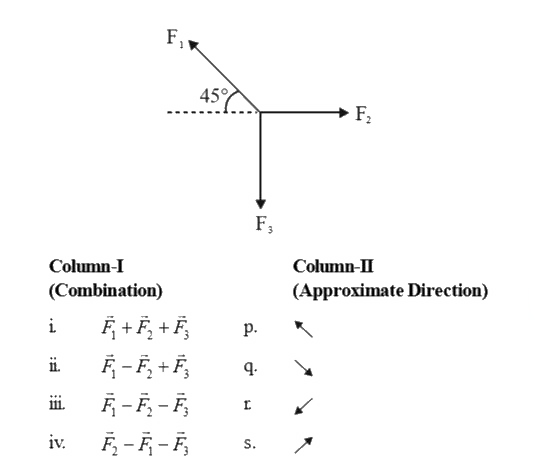
Now match the given columns and select the correct option from the codes given below.
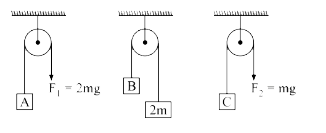
View SolutionIn the figure, blocks A, B and C of mass m each have acceleration a1, a2 and a3 respectively. F1 and F2 are external forces of magnitudes 2mg and mg respectively, then :
View Solution