Which of the following correspondences can be called a function ?
f(x)=x3,{−1,0,1}→{0,1,2,3}
f(x)=±√x,{0,1,2}→{−2,−1,0,1,2}
f(x)=√x,{0,1,4}→{−2,−1,0,1,2}
f(x)=−√x,{0,1,4}→{−2,−1,0,1,2}
The correct Answer is:C, D
To determine which of the given correspondences can be classified as a function, we need to apply the definition of a function. A correspondence f from a set X to a set Y is called a function if every element x in X has a unique image f(x) in Y. This means that:
1. Each element in X must map to one and only one element in Y.
2. It is acceptable for different elements in X to map to the same element in Y, but no element in X can map to multiple elements in Y.
Let's analyze each option step by step.
Step 1: Analyze the first option f(x)=x3
- For x=−1: f(−1)=(−1)3=−1
- For x=0: f(0)=03=0
- For x=1: f(1)=13=1
Conclusion: Each x maps to a unique f(x). Thus, this correspondence is a function.
Step 2: Analyze the second option f(x)=±√x
- For x=0: f(0)=±√0=0 (maps to 0)
- For x=1: f(1)=±√1=±1 (maps to both 1 and -1)
- For x=2: f(2)=±√2 (maps to both √2 and −√2)
Conclusion: Since x=1 maps to two different values (1 and -1), this correspondence is not a function.
Step 3: Analyze the third option f(x)=√x
- For x=0: f(0)=√0=0
- For x=1: f(1)=√1=1
- For x=4: f(4)=√4=2
Conclusion: Each x maps to a unique f(x). Thus, this correspondence is a function.
Step 4: Analyze the fourth option f(x)=−√x
- For x=0: f(0)=−√0=0
- For x=1: f(1)=−√1=−1
- For x=4: f(4)=−√4=−2
Conclusion: Each x maps to a unique f(x). Thus, this correspondence is a function.
Final Summary of Results:
- Option 1: Function
- Option 2: Not a function
- Option 3: Function
- Option 4: Function
2. It is acceptable for different elements in X to map to the same element in Y, but no element in X can map to multiple elements in Y.
- For x=0: f(0)=03=0
- For x=1: f(1)=13=1
- For x=1: f(1)=±√1=±1 (maps to both 1 and -1)
- For x=2: f(2)=±√2 (maps to both √2 and −√2)
- For x=1: f(1)=√1=1
- For x=4: f(4)=√4=2
- For x=1: f(1)=−√1=−1
- For x=4: f(4)=−√4=−2
- Option 1: Function
- Option 2: Not a function
- Option 3: Function
- Option 4: Function
Topper's Solved these Questions
- FUNCTIONBook:MOTIONChapter:FUNCTIONExercise:Exercise - 1 ( JEE Main)
Explore 48 Videos
- FUNCTIONBook:MOTIONChapter:FUNCTIONExercise:Exercise - 2 (Level-I)
Explore 33 Videos
- ELLIPSE Book:MOTIONChapter:ELLIPSE Exercise:Exercise - 4 | Level-I Previous Year | JEE Main
Explore 20 Videos
- HYPERBOLABook:MOTIONChapter:HYPERBOLAExercise:EXERCISE-4 (Level-II)
Explore 17 Videos
Similar Questions
Which of the following correspondences can not be called a function ?
f(x)=x3;{−1,0,1}−−−−−−−−−→−1,0,1,2,3
f(x)=±√x;{0,1,4}−−−−−−−−−−−−→−2,−1,0,1,2
f(x)=√x;{0,1,4}−−−−−−−−−−−−→−2,−1,0,1,2
f(x)=−√x;{0,1,4}−−−−−−−→−2,0,1,2
View SolutionWhich of the following sets can be called isoelectronic species ?
View Solution
Knowledge Check
Which of the following corresponds to one node ?
A B
B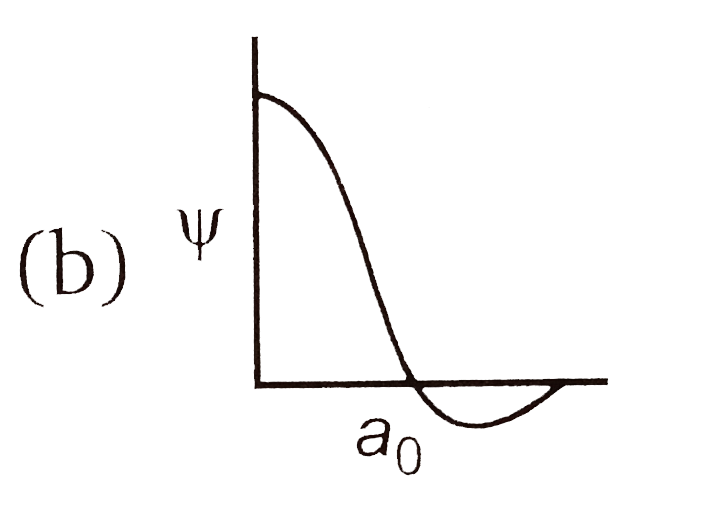 C
C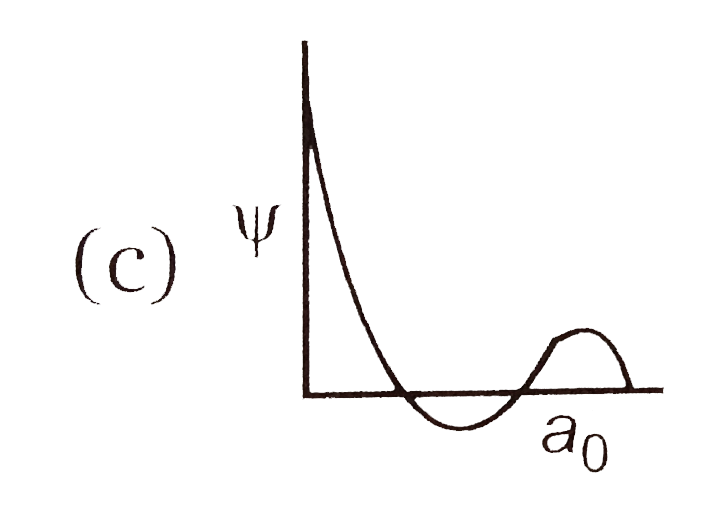 D
D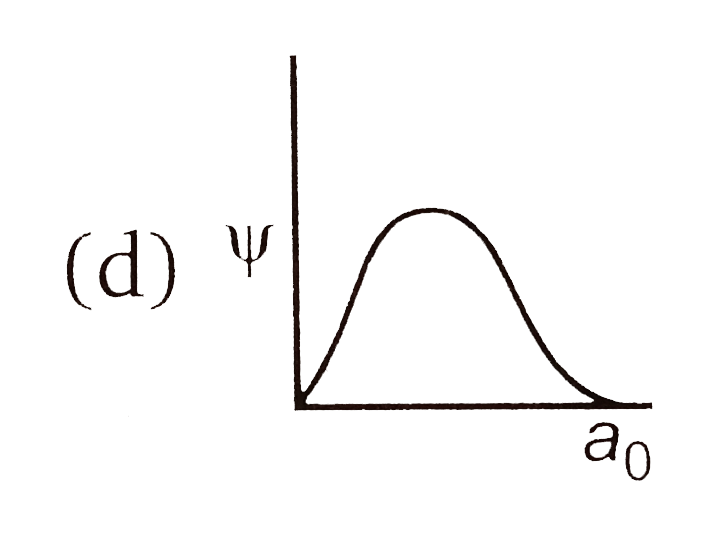
Which of the following corresponds to mutagens
AChemicals and radiations which cause changes in the genetic material of a cellBVarious archaebacteria that produce methaneCChemicals which react with ozone molecules and destroy themDRNA molecules that infect plant cells and cause diseasesWhich of the following noble gases do not reasct with function
AXeBHeCArDKr
Which of the following sets can be called isoelectronic species ?
View SolutionWhich of the following graphs correspond to one node ?
View SolutionWhich one of the following organ can be called a sort of ''blood bank''
View SolutionWhich of the following centre can moderate the functions of the respiratory rhythm centre
View SolutionWhich of the following can represent a linear function for each x∈R ?
View Solution