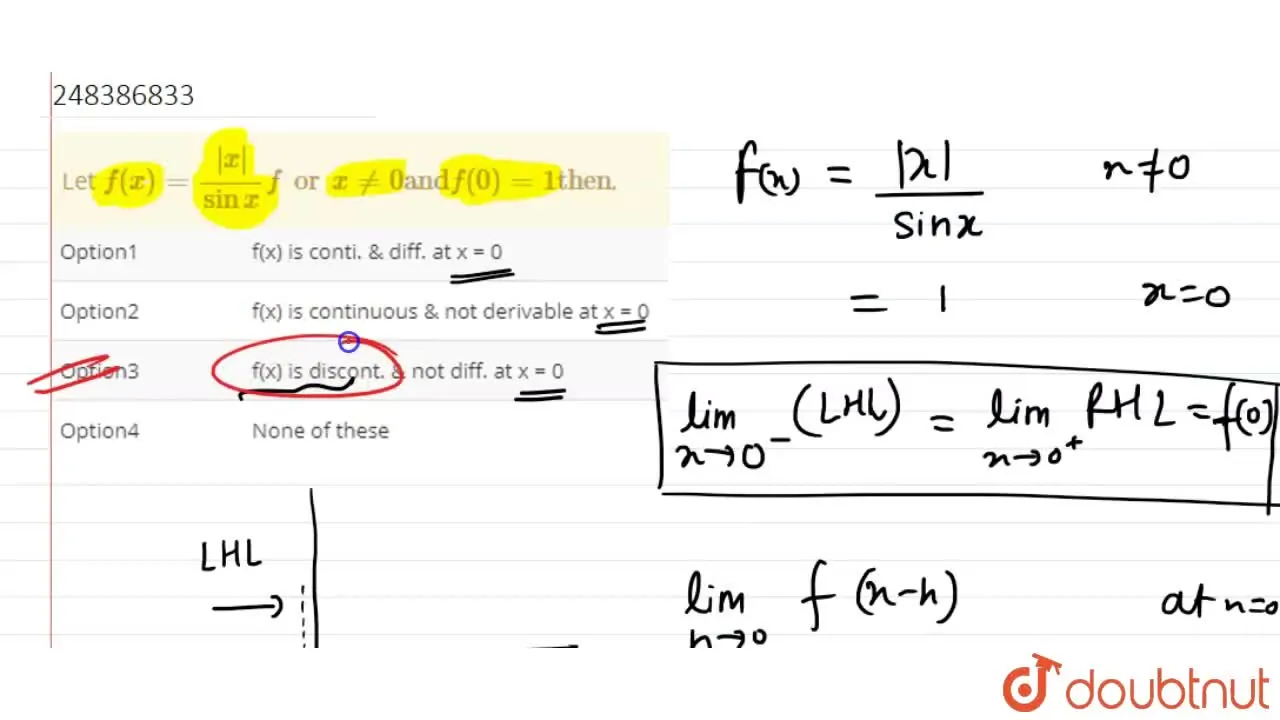Let f(x)=|x|sinxforx≠0andf(0)=1then,
f(x) is conti. & diff. at x = 0
f(x) is continuous & not derivable at x = 0
f(x) is discont. & not diff. at x = 0
None of these
Step by step video & image solution for Let f(x)=(abs(x))/(sinx) for xne0 "and" f(0)=1 "then", by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MOTIONCHAPTER - DIFFERENTIABILITYEXERCISE - Exercise - 2 (Level-I) Objective Problems | JEE Main15videos
DIFFERENTIABILITY
- BOOK - MOTIONCHAPTER - DIFFERENTIABILITYEXERCISE - Exercise - 2 (Level-II) Multiple Correct | JEE Advanced8videos
DIFFERENTIABILITY
- BOOK - MOTIONCHAPTER - DIFFERENTIABILITYEXERCISE - Exercise - 4 | Level-I Previous Year | JEE Main15videos
DIFFERENTIABILITY
- BOOK - MOTIONCHAPTER - DETERMINANTS EXERCISE - EXERCISE-4 (LEVEL-II)6videos
DETERMINANTS
- BOOK - MOTIONCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise 429videos
DIFFERENTIAL EQUATION
Similar Questions
Which one of the following is correct in respect of the function f(x)=x2|x| for x≠0and f(0)=0?
View SolutionConsider the following statements in respect of the function f(x)=sin(1x) for x≠0andf(0)=0
1. limx→0f(x) exists
2. f(x) is continuous at x = 0
Which of the above statements is/are correct?View SolutionIf f(x)=log(1+ax)−log(1−bx)x, for x≠0 and f(0)=k and f(x) is continuous at x=0, then k is equal to
View SolutionLet f(x) be a polynomial function satisfying f(x)+f(1x)=f(x)f(1x) for all x≠0. If f(5)=126 and a,b,c are in G.P., thenf'(a),f'(b),f'(c) are in
View SolutionIf f(x)=log(sec2x)cot2x for x≠0 and k for x=0 is continuous at x=0, then k is
View SolutionThe function f(x)=x2sin1x, x≠0,f(0)=0 at x=0
View SolutionGiven f(0)=(0) and f(x)=1(1−e−1/x) for x≠0. Then, only one of the following statements on f(x) is true. That is f(x) is
View SolutionLet f(x)=√1+sinx−√1−sinxtanx,x≠0 Then limx→0f(x) is equal to
View SolutionDiscuss the continuity of f(x) at x = 0 if :
f(x)={√1+x−√1−xsinx, if x≠01 , if x=0.View SolutionLetf(x)=⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦,then (A) (f(x))2=−I (B) f(x+y)=f(x),f(y) (C) f(x)−1=f(−x) (D) f(x)−1=f(x)
View Solution