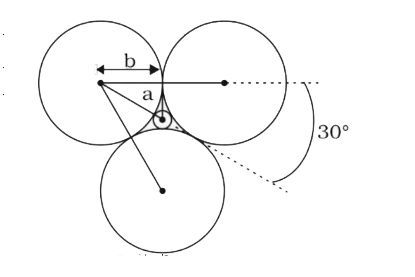
Find the critical radius ratio for triangular void
The correct Answer is:rR=0.155
To find the critical radius ratio for triangular voids, we can follow these steps:
1. Understanding the Structure:
Triangular voids are formed when three spheres are arranged in such a way that they create a triangular shape. The coordination number for this arrangement is 3.
2. Defining Distances:
- The distance between the centers of two adjacent spheres is denoted as 2r (where r is the radius of the spheres).
- The distance from the center of one sphere to the center of the void formed is r+r=2r.
3. Using Geometry:
- In the triangular arrangement, we can visualize the triangle formed by the centers of the three spheres. The angle at the center of the void is 30∘.
- We can apply the cosine rule in this triangle.
4. Applying the Cosine Function:
- Using the cosine of the angle, we have:
cos(30∘)=BaseHypotenuse=rr+r
- Here, the base is r and the hypotenuse is r+r=2r.
5. Calculating the Cosine Value:
- We know that cos(30∘)=√32. Therefore, we can set up the equation:
r2r=√32
6. Rearranging the Equation:
- This simplifies to:
r=√32⋅2r
- Which leads to:
1=√3
7. Finding the Critical Radius Ratio:
- Rearranging gives us:
r+r=2r=2√3R
- Thus, we can express the critical radius ratio as:
rR=1√3≈0.577
8. Final Result:
- The critical radius ratio for triangular voids is approximately 0.577.
Triangular voids are formed when three spheres are arranged in such a way that they create a triangular shape. The coordination number for this arrangement is 3.
- The distance between the centers of two adjacent spheres is denoted as 2r (where r is the radius of the spheres).
- The distance from the center of one sphere to the center of the void formed is r+r=2r.
- In the triangular arrangement, we can visualize the triangle formed by the centers of the three spheres. The angle at the center of the void is 30∘.
- We can apply the cosine rule in this triangle.
- Using the cosine of the angle, we have:
cos(30∘)=BaseHypotenuse=rr+r
- Here, the base is r and the hypotenuse is r+r=2r.
- We know that cos(30∘)=√32. Therefore, we can set up the equation:
r2r=√32
- This simplifies to:
r=√32⋅2r
- Which leads to:
1=√3
- Rearranging gives us:
r+r=2r=2√3R
- Thus, we can express the critical radius ratio as:
rR=1√3≈0.577
- The critical radius ratio for triangular voids is approximately 0.577.
Topper's Solved these Questions
- CLASSROOM PROBLEMS Book:MOTIONChapter:CLASSROOM PROBLEMS Exercise:Mole Concept
Explore 29 Videos
- CLASSROOM PROBLEMS Book:MOTIONChapter:CLASSROOM PROBLEMS Exercise:Ionic Equilibrium
Explore 35 Videos
- CLASSROOM PROBLEMS Book:MOTIONChapter:CLASSROOM PROBLEMS Exercise:Radioactivity
Explore 23 Videos
- Chemical KineticsBook:MOTIONChapter:Chemical KineticsExercise:Exercise - 4 (Level - II) (SUBJECTIVE PROBLEM)
Explore 1 Video
- CLASSROOM PROBLEMS 1Book:MOTIONChapter:CLASSROOM PROBLEMS 1Exercise:THERMODYNAMICS
Explore 17 Videos
Similar Questions
Knowledge Check
The limiting radius ratio for tetrahedral voids has the range:
A0.414 to 0.732B0.225 to 0.414C0.155 to 0.225D0 to 0.155In a close-packed structure, if r is the radius of the spherical void and R is the radius of the spheres forming voids, the critical r/R value for the tetrahedral void is equal to
A0.155B0.225C0.414D0.732Find the radius of an equilateral triangular plate about its median. Side of triangular is l.
Al√12Bl√24Cl√96Dl√48
Find out the ratio of maximum number of triangular voids and rectangular voids formed by nine atoms according to HCP and square close packing in 2D respectively
View SolutionLimiting radius ratio|Calculation of limiting radius ratio for different voids
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
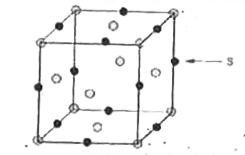
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View Solution