For 2Ak1−−→Bk2−−→3C.K1=2×10−4sec−1andk2=3×10−4/mol-sec. {d[B]/dt} equal to :
k1[A]−k2[B]
k1[A]2−k2[B]
k1[A]−k2[B]2
k1[A]2−k2[C]3
The correct Answer is:C
To solve the problem, we need to find the rate of change of concentration of species B, denoted as d(B)dt, for the given reactions:
1. 2Ak1→B
2. Bk2→3C
Where:
- k1=2×10−4s−1 (first-order reaction)
- k2=3×10−4mol−1s−1 (second-order reaction)
1. Identify the Rate of Formation of B:
The formation of B from A is given by the rate equation:
Rate of formation of B=k1(A)2
Since the stoichiometry of the reaction is 2A→B, we use (A)2 because two moles of A are consumed to produce one mole of B.
2. Identify the Rate of Consumption of B:
The consumption of B to form C is given by the rate equation:
Rate of consumption of B=k2(B)2
Here, B is consumed in a second-order reaction, hence the (B)2 term.
3. Write the Net Rate of Change of B:
The net rate of change of concentration of B is the difference between the rate of formation and the rate of consumption:
d(B)dt=Rate of formation of B−Rate of consumption of B
Substituting the expressions from steps 1 and 2:
d(B)dt=k1(A)2−k2(B)2
4. Final Expression:
Thus, the final expression for the rate of change of concentration of B is:
d(B)dt=k1(A)2−k2(B)2
2. Bk2→3C
- k1=2×10−4s−1 (first-order reaction)
- k2=3×10−4mol−1s−1 (second-order reaction)
The formation of B from A is given by the rate equation:
Rate of formation of B=k1(A)2
Since the stoichiometry of the reaction is 2A→B, we use (A)2 because two moles of A are consumed to produce one mole of B.
The consumption of B to form C is given by the rate equation:
Rate of consumption of B=k2(B)2
Here, B is consumed in a second-order reaction, hence the (B)2 term.
The net rate of change of concentration of B is the difference between the rate of formation and the rate of consumption:
d(B)dt=Rate of formation of B−Rate of consumption of B
Substituting the expressions from steps 1 and 2:
d(B)dt=k1(A)2−k2(B)2
Thus, the final expression for the rate of change of concentration of B is:
d(B)dt=k1(A)2−k2(B)2
Topper's Solved these Questions
- Chemical KineticsBOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 2 (Level-I) (Mechanism of reaction and theories of reaction rate)
3 Videos
- Chemical KineticsBOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 2 (Level-II) (Introduction, Rate of reaction, Factor affecting rate of reaction, Effect of concentration on reaction rate)
3 Videos
- Chemical KineticsBOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 2 (Level-I) (Arrhenius equation)
11 Videos
- CHEMICAL EQUILIBRIUMBOOK - MOTIONCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise - 4
20 Videos
- CLASSROOM PROBLEMS BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Electrochemistry
22 Videos
Similar Questions
The substance undergoes first order decomposition. The decomposition follows two parallel first order reactions as :
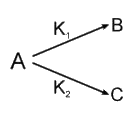
K1=1.26×10−4sec−1andK2=3.8×10−5sec−1 The percentage distribution of B and C
View SolutionA substance undergoes first order decomposition. The decomposition follows two parallel first order reactions as
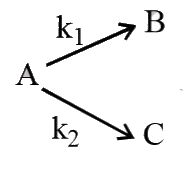, k1=1.26×10−4 sec−1andk2=3.6×10−5 sec−1 Calculate the % distribution of B & C.
View Solution
Knowledge Check
A consecutive reaction, AK1−−→BK2−−→C is characterised by:
AMaximum in the concentration of ABMaximum in the concentration of BCMaximum in the concentration of CDHighly exothermicityConisder the following reactions:
I. A+Bk1⇐⇒k−1C
II. C+Bk2−−→D
Then k1[A][B]−k−1[C]−k2[C][B] is equal toA−d[A]dtB−d[B]dtCd[C]dtDd[D]dtIn the sequence of reaction,
Lk1−−→Mk2−−→Nk3−−→O
k3>k2>k1
The rate determining step of the reaction is :AL→MBM→NCN→ODL→O
Mechanism of the reaction is:
Ak1−−→B,2Ak2−−→C+D
What is −d[A]dt ?
View SolutionMechanism of the reaction is:
A2k1⇐⇒2A
A+Bk2−−→C
A2+Ck−−→D+A
What is (a) −d[A2]dt, (b) −d[A]dt, (c ) d[C]dt, (d) d[D]dt ?
View SolutionFor a reversible first-order reaction,
AK1⇐===⇒K2B,Kf=10−2s−1andBeq.Aeq.=4,
If A0=0.01ML−1 and B0=0, what will be concentration of B after 30sec?
View SolutionMechanism of the reaction is:
A2k2⇐⇒2A
A+Bk2−−→C
A2+Ck−−→D+A
What is (a) −d[A2]dt, (b) −d[A]dt, (c ) d[C]dt, (d) d[D]dt ?
View SolutionA radioactive element decays by following three different parallel paths :
Aλ1−−→B,λ1=5×10−2sec−1
2Aλ2−−→C,λ2=3×10−2sec−1
3Aλ3−−→D,λ3=5×10−3sec−1
Calculate average life- time of element (in sec.)
[λ1,λ2,λ3are decay constans for respective reactions]
View Solution