For a first order reaction A(g)→2B(g)+C(g) at constant volume and 300 K, the total pressure at the beginning (t=0) and at time t ae P0andPt respectively. Initially, only A is present with concentration [A]0andt1/3 is the time required for the partial pressure of A to reach 1/3rd of its initial value. The correct options (s) is (are) :
(Assume that all these behave as ideal gases)
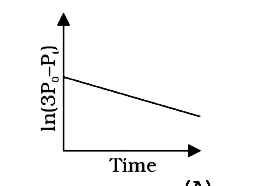
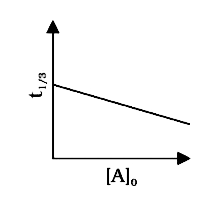

The correct Answer is:A, D
A(g)→2B(g)+C(g)
First order reaction
A(g)→2B(g)+C(g)
t=0 [A]o − −
t=t [A]o−x 2x x
[Ao]+2x αPt
2x α (Pt−Po)
x α (Pt−Po)2
In AoAt=kt⇒ In AoAo−x=kt
⇒ In PoPo−[Pt−Po2]=kt⇒ In 2Po3Po−Pt=kt⇒ In 2Po− In (3Po−Pt)=kt
⇒ In ⎛⎜⎝3↓yPo−Pt⎞⎟⎠= In 2↓CPo−kt↓mx (so slope =-k (-ve))
⇒ t1/2=1kln3,t1/3 is independent of [A]o , k is constant.
Similar Questions
For a gas phase first order reaction,
A(g)→B(g)+2C(g)+D(g)
The initial pressure was P0 While pressure after 't' time becomes Pt (Pt>P0). The expression for the rate constant (K) would be
View SolutionConsider a first order reaction at "450K
X(g)→Y(g)+Z(g)
What is the rate constant of the reaction using given data? [Assume initially only X is present ]
[Time(s)05( Total Pressure )1520]
View Solution
Knowledge Check
For a first order reaction A(g)→2B(g)+C(g) at constant volume and 300 K, the total pressure at the beginning (t=0) and at time t and P0 and Pt respectively, Initially, only A is present with concentration [A]0 and t1/3 is the required for the partial pressure of A to reach 1/3rd of its initial value. The correct option(s) is are
(Assume that all these gases behave as ideal gases)A B
B C
C D
D
For a first order reaction A(g)→2B(g)+C(g) at constant volume and 300 K, the total pressure at the beginning (t=0) and at time t ae P0andPt respectively. Initially, only A is present with concentration [A]0andt1/3 is the time required for the partial pressure of A to reach 1/3rd of its initial value. The correct options (s) is (are) :
(Assume that all these behave as ideal gases)A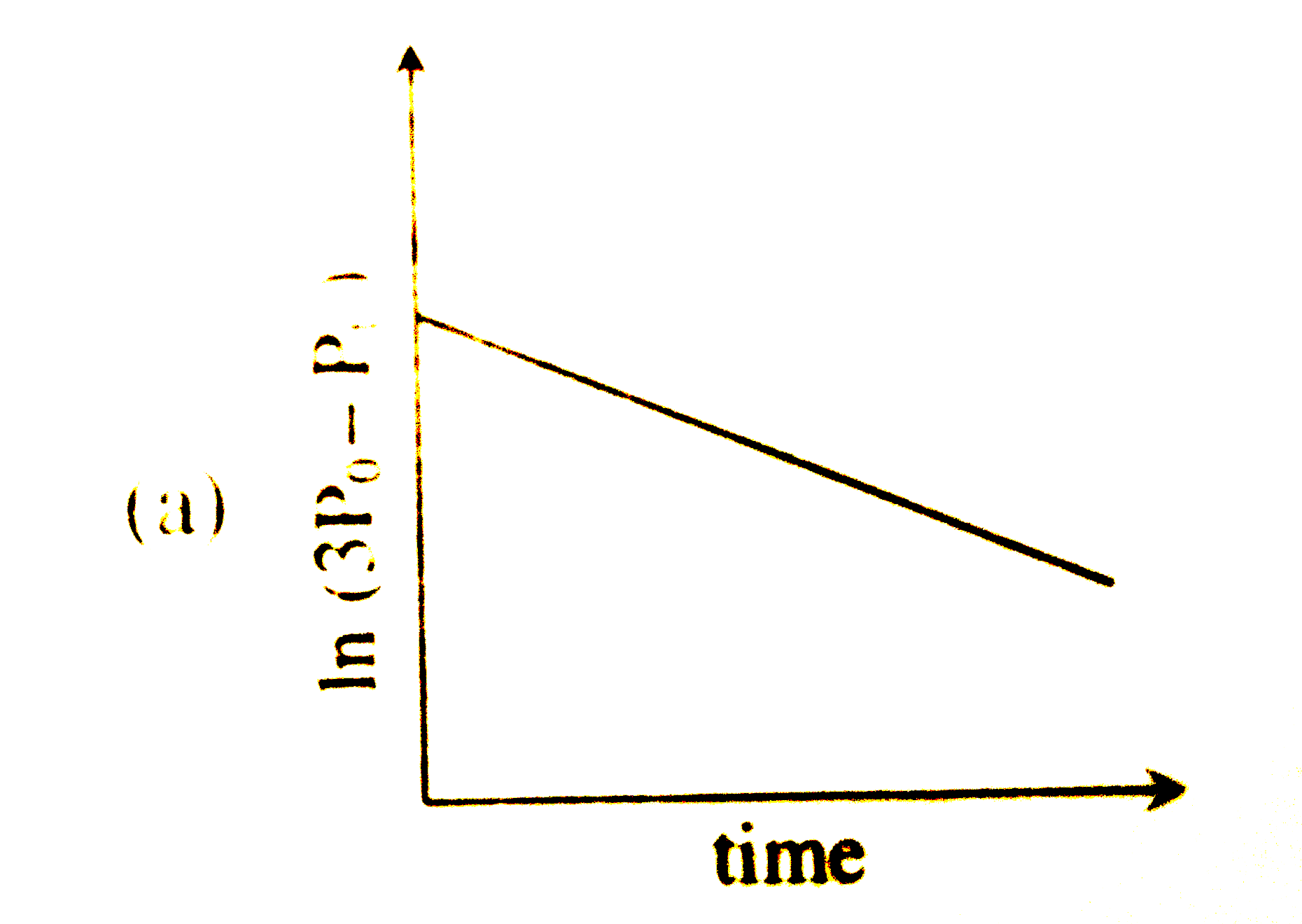 B
B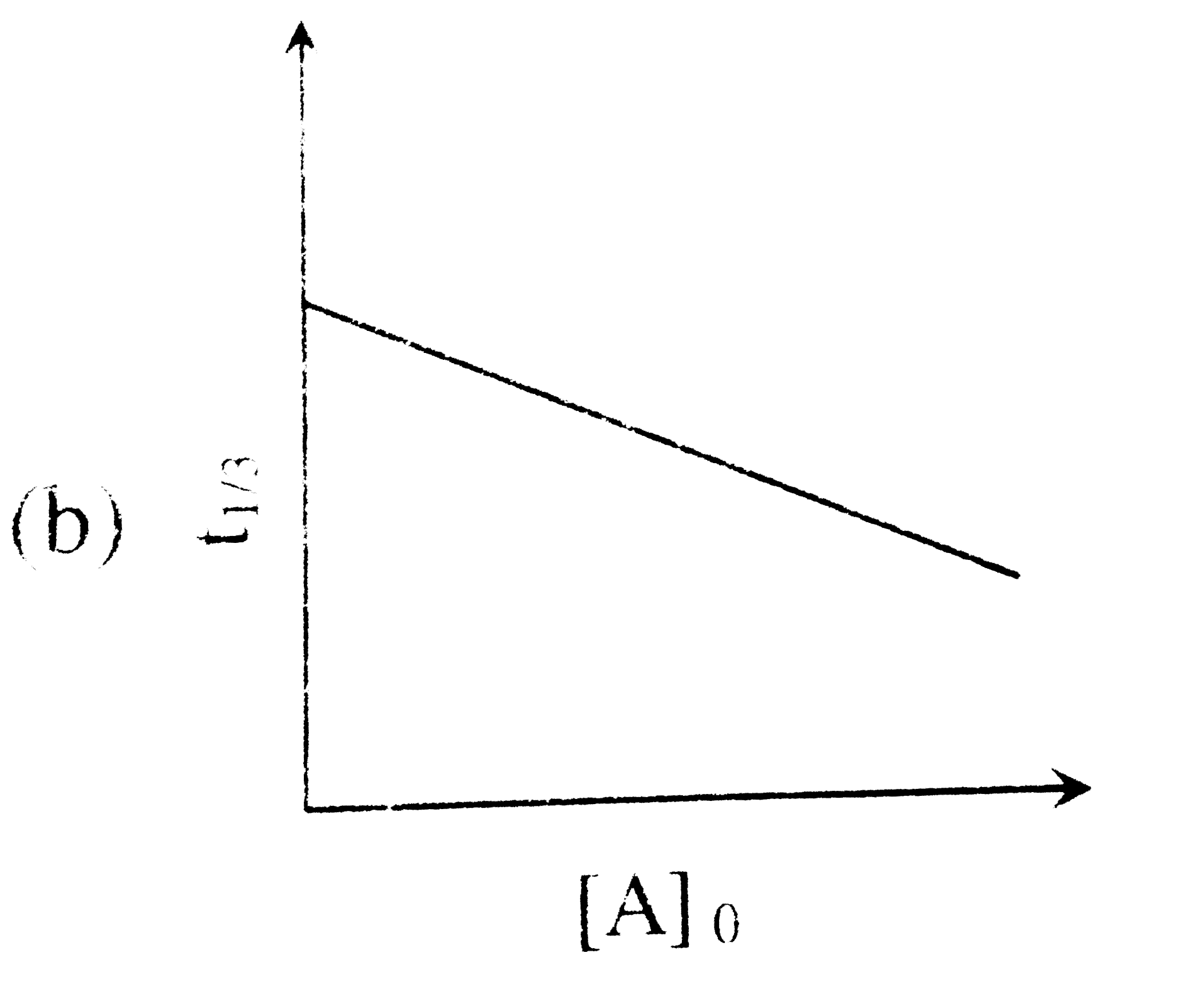 C
C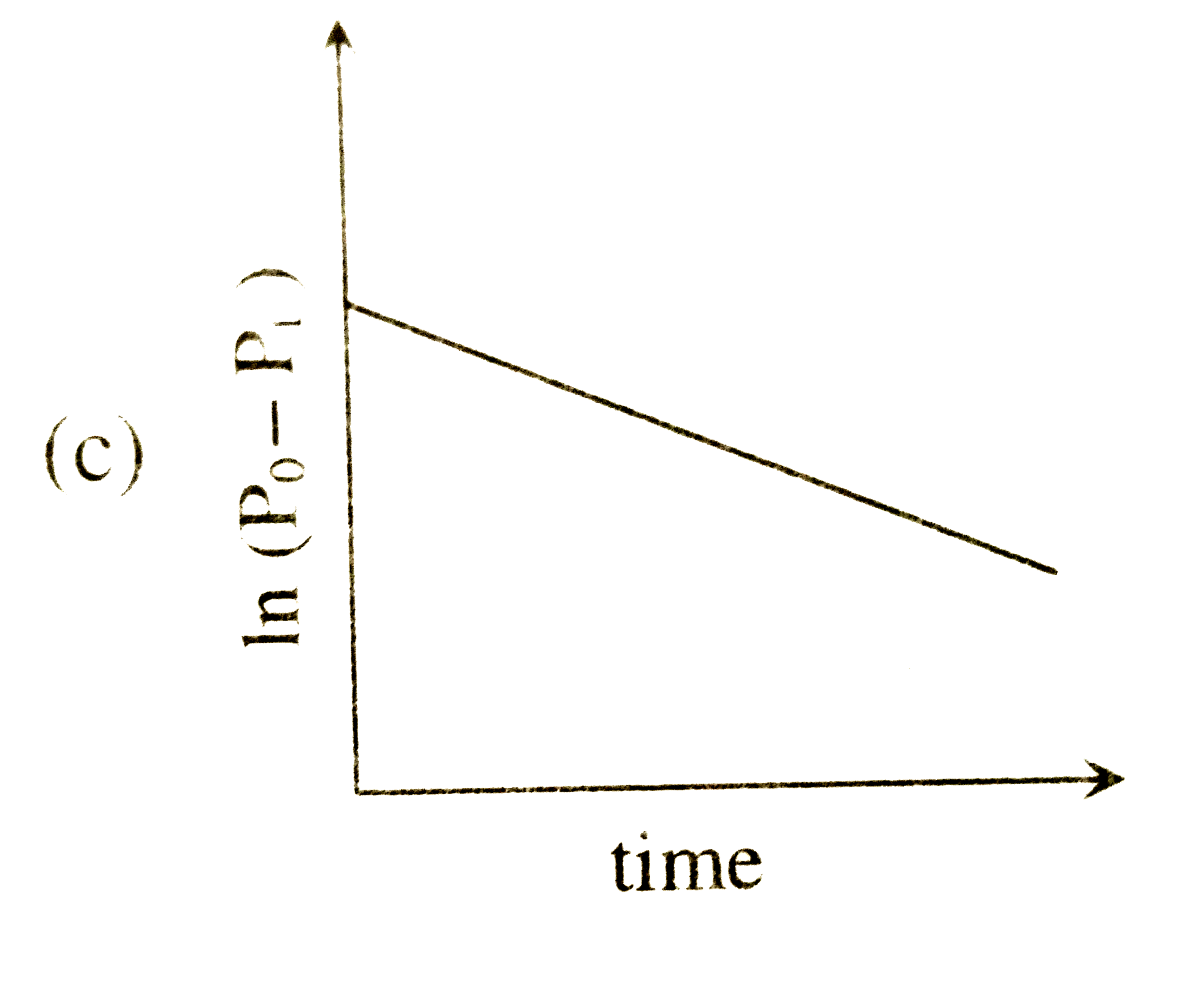 D
D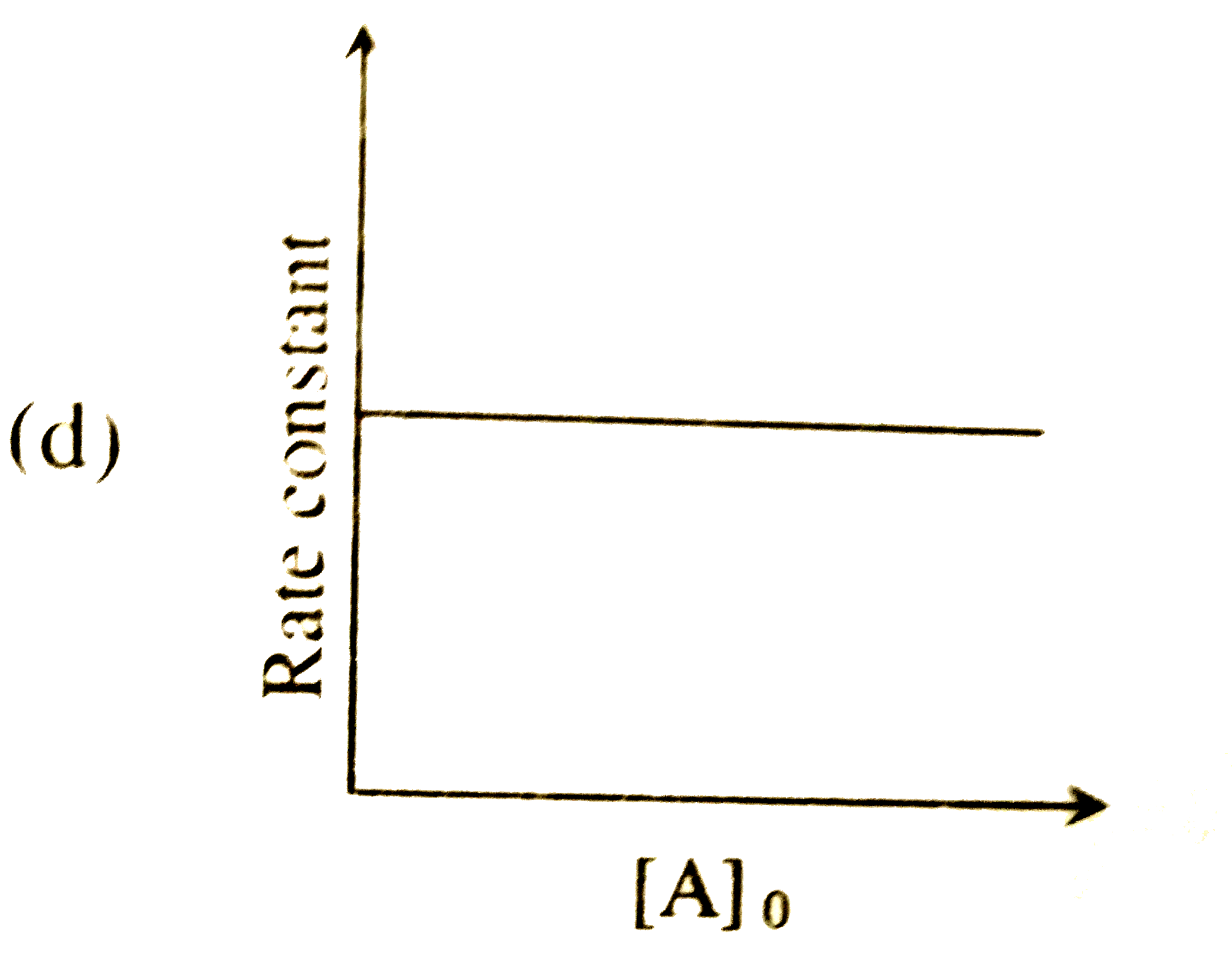
For a first order gas phase reaction :
A(g)→2B(g)+C(g)
P0 be initial pressure of A and Pt the total pressure at time 't'. Integrated rate equation is :A2.303tlog(P0P0−Pt)B2.303tlog(2P03P0−Pt)C2.303tlog(P02P0−Pt)D2.303tlog(2P02P0−Pt)
For the first order reaction A(g)→2B(g)+C(g), the initial pressure is PA=90 mm Hg, the pressure after 10 minutes is found to be 180 mm Hg. The rate constant of the reaction is
View SolutionFor the first order gas phase decomposition reaction,
A(g)→B(g)+C(g)
if P0 is the initial pressure of A and Pt is total pressure after time t, then
View SolutionFor a first order reaction :
A(g) → B(g) + C(g)+ D(g)
Occurring at 1 bar pressure and 300 K if initial volume of the container containing only A is V0 and after 10 minutes it is V10 then average life of A will be (in minutes) :
View SolutionIn a first-order reaction of the type: A(g)→2B(g), the initial and final pressures are P1 and p respectively. The rate constant can be expressed by
View SolutionFor a first order reaction R→P, the rate constant is k. if the initial concentration of R is [R0], the concentration of R at any time 't' is given by the expression-
View Solution
