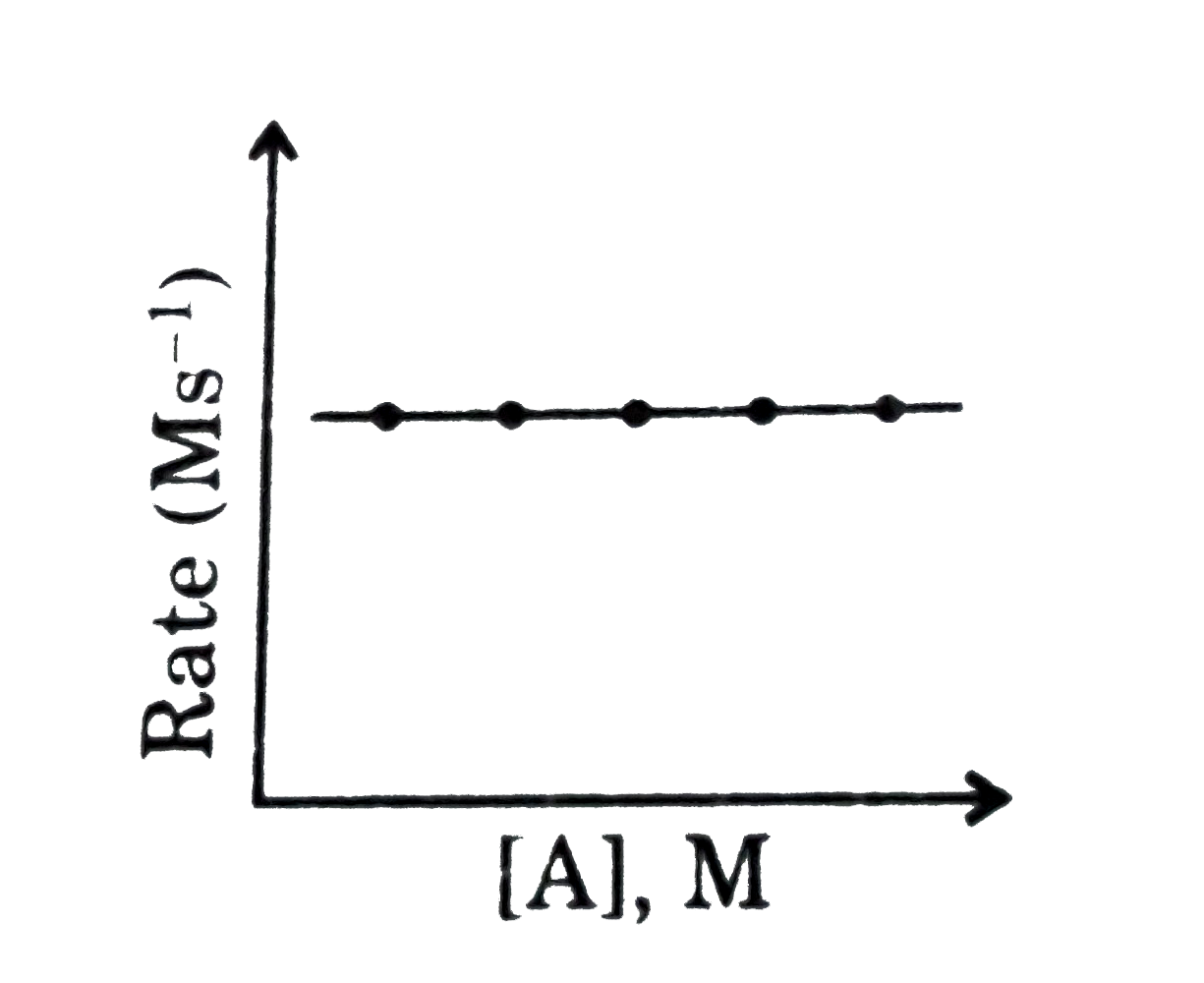
Following reaction can take place in both direction Ak1k2B. For the forward reaction and for the backward direction
[B]Rate0.01M1×10−2Ms−10.02M2×10−2Ms−1
Hence, net reaction rate is :
![Following reaction can take place in both direction A {:(k(1)),(k(2)):}B. For the forward reaction and for the backward direction {:([B],](https://d10lpgp6xz60nq.cloudfront.net/physics_images/VMC_CHE_WOR_BOK_04_C18_E03_048_Q01.png)
=k1[A]−k2[B]
=k1−k2[B]
=k1[A]−k2
=k1−k2
The correct Answer is:B
Based on (A), rate is independent of (A) and when (B) is doubled, rate is also doubled.
Thus, for forward reaction rate law =k1[A]o=k1 and for backward reaction are law =k2[B]
Thus, net rate =k1−k2[B]
Similar Questions
Knowledge Check
Following reaction can take place in both direction Ak1⇐⇒k2B. Graph is given for the forward reaction. And for the beackward reaction, following data is obtained:
[B]Rate0.01M1×10−2Ms−10.02M2×10−2Ms−1
Hence, net reaction rate of B is:A=k1[A]−k2[B]B=k1−k2[B]C=k1[A]−k2D=k1−k2The rate constant for a reaction is 2×10−2s−1 at 300 K and 8×10−2s−1 at 340 K The energy of activation of the reaction is
A14.695 kJ mol−1B29.39 kJ mol−1C44kJmol−1D22kJmol−1For a reaction aA+bB→ products the following data were found
[A][B]rate0.100.101×10−20.200.208×10−20.100.202×10−2
The overall order of reaction isA3B1CzeroD2
For a given reaction A→ Product, rate is 1×10−4Ms−1 when [A]=0.01M and rate is 1.41×10−4Ms−1 when [A]=0.02M. Hence, rate law is :
View SolutionFor a first order reaction, A → products, the rate of reaction at [A] = 0.2 M is 1.0×10−2 mol litre−1−1min. The half-life period for the reaction is
View SolutionFor a given reaction,
A→Product, rate is1×10−4Ms−1
when [A] = 0.01 M and rate is 1.41×10−4M s−1
when[A] = 0.02 M. Hence, rate law is :
View SolutionFor the reaction , A+2B⇔2C, the rate constant for the forward and the backward reactions are 1×10−4 and 2.5×10−2 respectively.The value of equilibrium constant, K, for the reaction would be :
View SolutionFor a I order reaction A→B the reaction rate at reactant concentration 0.01 M is found to be 2.5×10−5Ms−1. The half life period of the reaction is
View Solution
