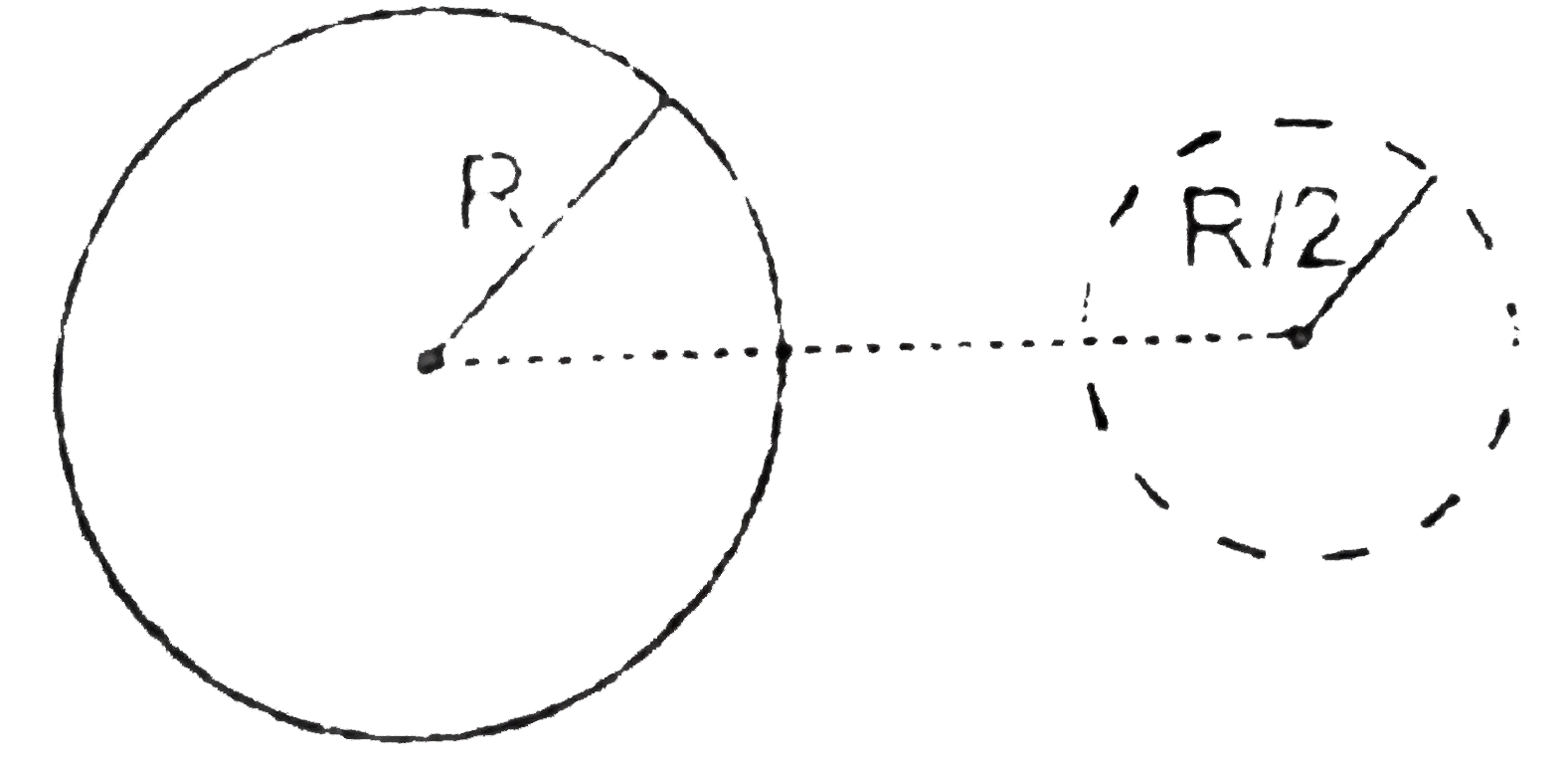
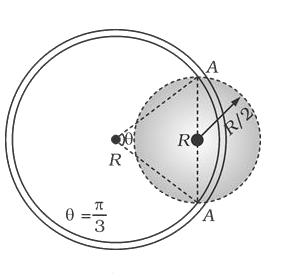
A ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
The correct Answer is:D
Electric flux will be maximum when maximum length of ring is inside the sphere. This will occur when the length of the chord AB is maximum. Now maximum length of chord AB can be the diameter of the ring. In this case of the arc of ring inside the sphere subtends an angle of at the centre of ring. Thus charge on this arc in this situation is given as
q=Rπ3.λ⇒ϕ=Rπ3e0λ=Rπλ3e0
Similar Questions
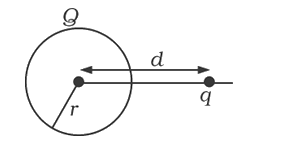
A solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :
View SolutionA quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View Solution
Knowledge Check
A half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
Aλ4εoln0Bλ4π2ε0rCλ4πε0rDλ4πε0r2Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If √8R is the distance between the centres of a ring (of mass 'm') and a sphere (mass "M") where both have equal radius "R'
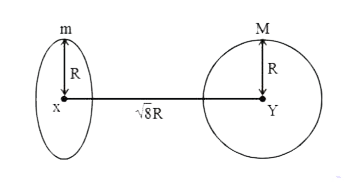 A√89.GmMRB2√23.GMmR2C13√8.GMmR2D√827.GmMR2
A√89.GmMRB2√23.GMmR2C13√8.GMmR2D√827.GmMR2Flux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
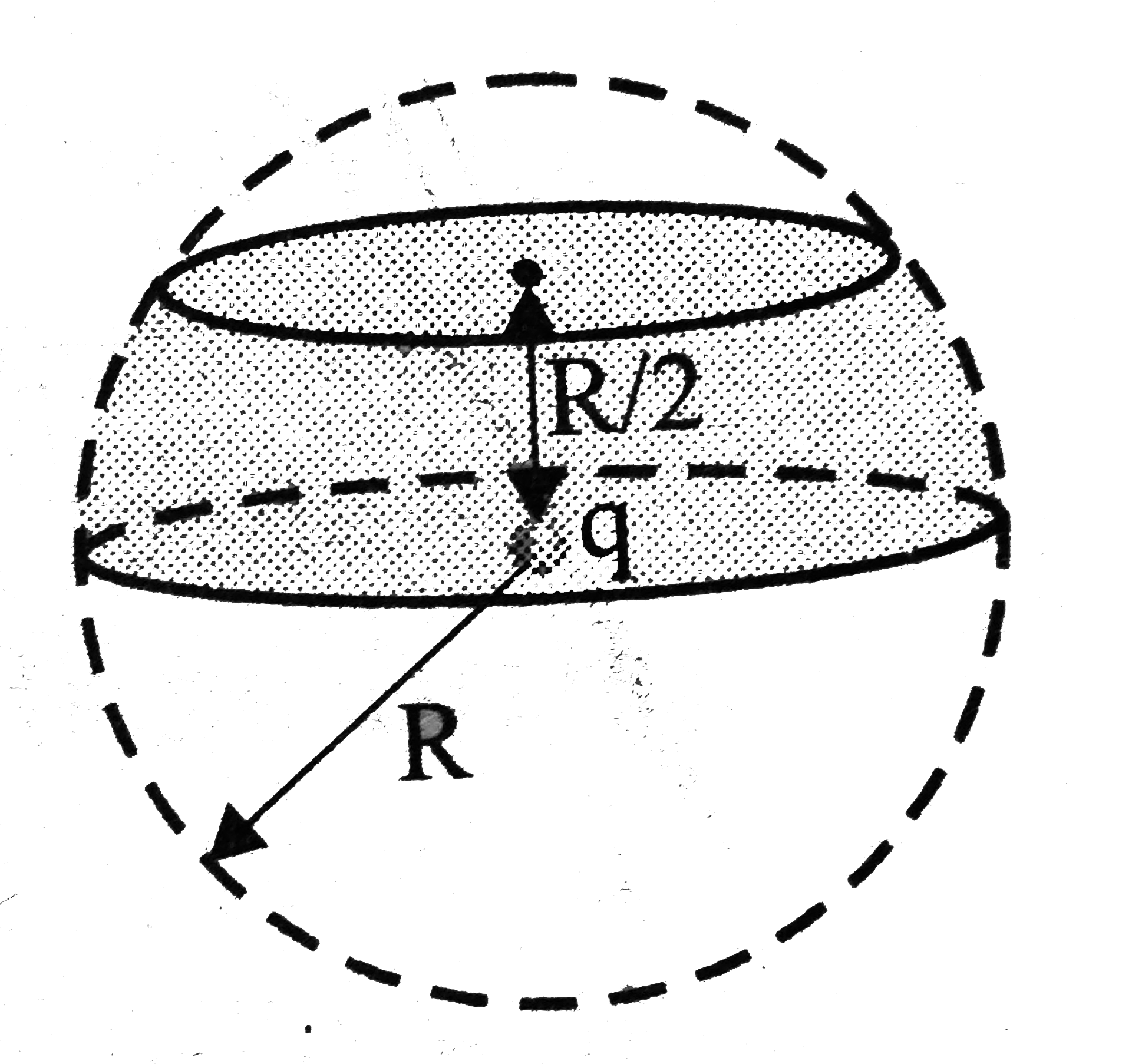 Aqε0Bq2ε0Cq4ε0Dzero
Aqε0Bq2ε0Cq4ε0Dzero
Three identical spheres each of mass M and radius R are arranged in a row touching each other and their centres collinear.The moment of inertia of the system about an axis passing through the centre of the middle sphere and perpendicular to the line joining their centres is "
View SolutionA sphere of radius R and charge Q is placed inside an imaginary sphere of radius 2R whose centre coincides with the given sphere. The flux related to imaginary sphere is:
View SolutionThe radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionThere is a ring of radius r having linear charge density λ and rotating with a uniform angular velocity ω. the magnetic field produced by this ring at its own centre would be
View Solution