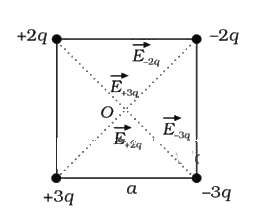
Four charge and are kept in the comers of a square of side . The total field at the centre of , find .
The correct Answer is:A, D
Similar Questions
Four charges +q,+2q,+3q and +4q are placed at the four corners ABCD of a square of side a. Calculate the field and potential at the centre of the square.
View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View Solution
Knowledge Check
Four charges of same magnitude q are placed at four corners of a square of side a . The value electric potential at the centre of the square will be (where k = 14πε0 )
A4kqaB4√2kqaC4kq√2aDkqa√2Point charges g, -q, 2Q and Q are placed in order at the corners A, B, Cand D of a square of side 2b. If the field at the midpoint of CD is zero, then qQ is
A1B2C2√25D5√52There are four point charges +q,−q,+q and −q are placed at the corners A,B,C and D respectively of a square of side a. The potential energy of the system is 14πε0 times
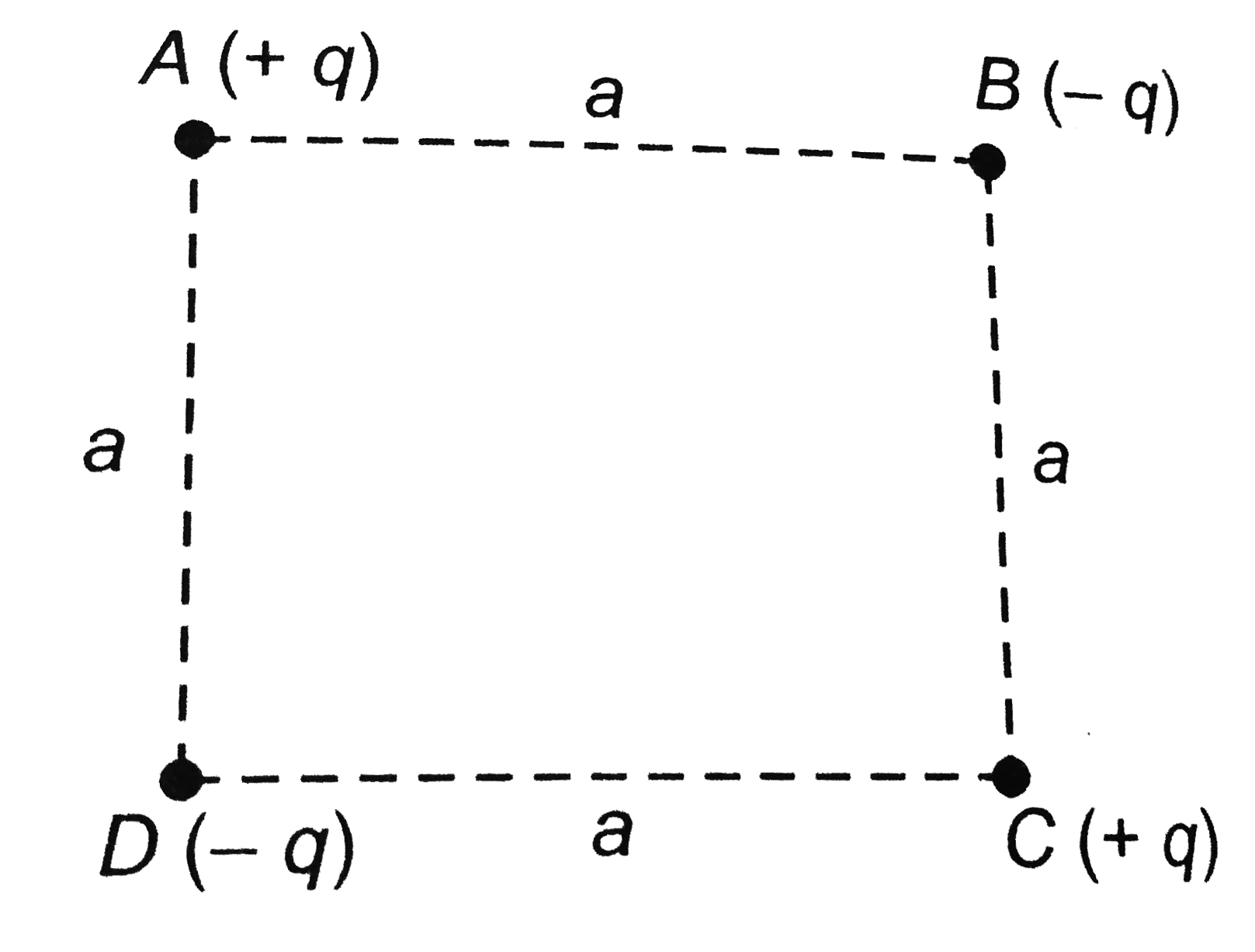 Aq2a(−4+√2)Bq22a(−4+√2)C4q2aD−4√2q2a
Aq2a(−4+√2)Bq22a(−4+√2)C4q2aD−4√2q2a
Four point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
resultant electric force on a charge Q
View SolutionFour electric charges +q,+q,−q and −q are placed at the corners of a square of side 2L (see figure). The electric potential at point A, mid-way between the two charges +q and +q, is

View Solutionq,2q, 3q and 4q charges are placed at the four corners A,B,C and D of a square. The field at the centre P of the square has the direction parallel to

View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View SolutionFour electric charges +q,+q,−q and −q are placed at the corners of a square of side 2L (see figure). The electric potential at point A, mid-way between the two charges +q and +q, is

View Solution