A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $ω$ is an example of non=inertial frame of reference. The relationship between the force ${\to F}_{r o t}$ experienced by a particle of mass m moving on the rotating disc and the force ${\to F}_{\in}$ experienced by the particle in an inertial frame of reference is
${\to F}_{r o t} = {\to F}_{i n} + 2 m ({\to v}_{r o t} \times \to ω) + m (\to ω \times \to r) \times \to ω$ .
where ${\to v}_{r o t}$ is the velocity of the particle in the rotating frame of reference and $\to r$ is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed $ω$ about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis $(\to ω = ω ˆ k)$ . A small block of mass m is gently placed in the slot at $\to r (R / 2) ˆ i$ at $t = 0$ and is constrained to move only along the slot.

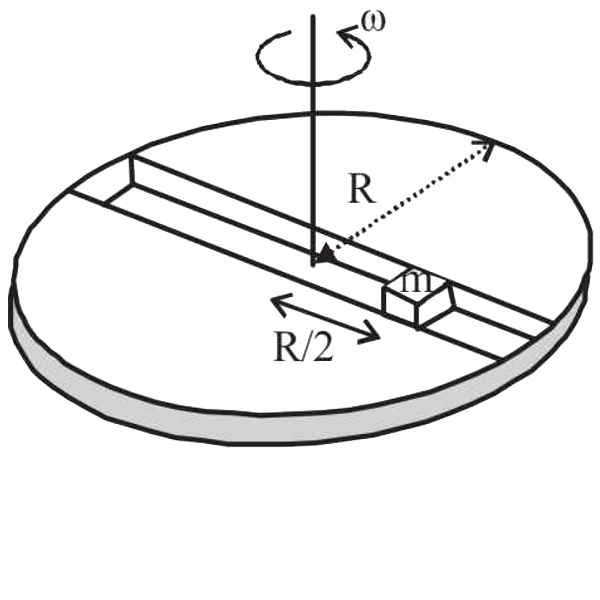
The net reaction of the disc on the block is

$m ω^{2} R sin ω t ˆ j - m g ˆ k$

$\frac{1}{2} m ω^{2} R (e^{ω t} - e^{- ω t}) ˆ j + m g ˆ k$

$\frac{1}{2} m ω^{2} R (e^{2 ω t} - e^{- 2 ω t}) ˆ j - m g ˆ k$

$- m ω^{2} R cos ω ˆ j - m g ˆ k$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023