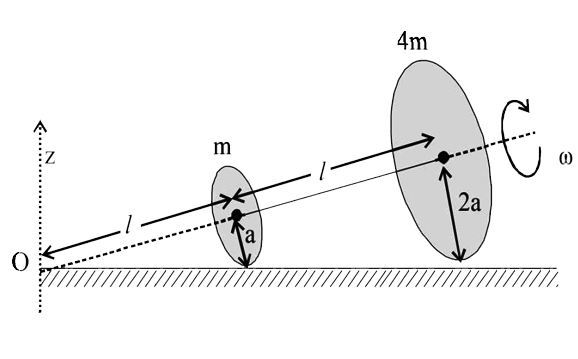
Two thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a massless, rigid rod of length l=√24a through their centres. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is ω. The angular momemtum of the entire assembly about the point 'O' is vacL (see the figure). Which of the follwing statement (s) is (are) true?
The correct Answer is:C, D

(i) Lz=ICM−0cosθ−LD−CMsinθ
=81√2425a2mω×√245−17ma2ω2×1√24
=81×24ma2ω25−17ma2ω2√24
(ii) LCM−0=(5m)[915ω]9l5=81mI2ω5,=81mI25×aωI
LCM−0=81mlaω5=81√24a2mω5
(iii) Velocity of point P:aω=1ω then,
ω=aω1 =Angular velocity of C.M. w.r.t. point O.
Angular velocity of CM w.r.t. Z-axis = ωcosθ
ωCM−z=aω1√245=aω√24a√245,ωCM−z=aω5
(iv) LD−CM=ma22ω+4m(2a)22ω=17ma2ω2
Similar Questions
A disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :
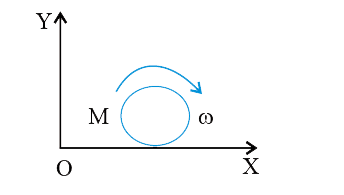
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View Solution
Knowledge Check
Two thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a massless, rigid rod of length l=√24a through their centres. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is ω. The angular momentum of the entire assembly about the point 'O' is →L (see the figure). Which of the following statement (s) is (are) true?
 AThe centre of mass of the assembly rotates about the z-axis with an angular speed of ω/5BThe magnitude of angular momentum of center of mass of the assembly about the point O is 81ma2ωCThe magnitude of angular momentum of the assembly about its center of mass is 17ma2ω/2Dthe magnitude of the z-componet of vacLis55ma2ω.
AThe centre of mass of the assembly rotates about the z-axis with an angular speed of ω/5BThe magnitude of angular momentum of center of mass of the assembly about the point O is 81ma2ωCThe magnitude of angular momentum of the assembly about its center of mass is 17ma2ω/2Dthe magnitude of the z-componet of vacLis55ma2ω.A sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
A45Mv0R(−ˆk)B95Mv0R(−ˆk)C85Mv0R(−ˆk)D75Mv0R(−ˆk)A uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.
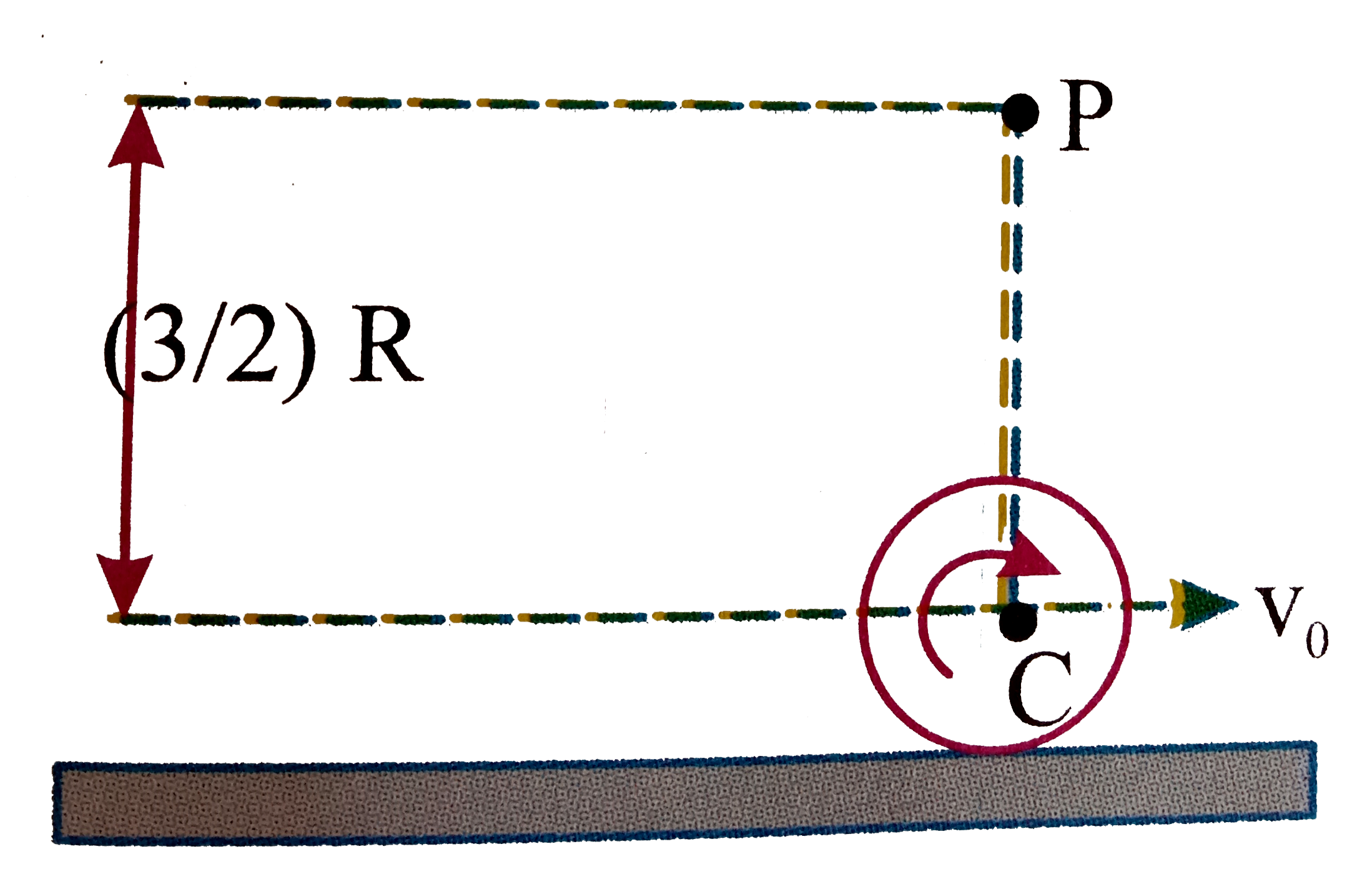 Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0
Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0
Two uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View Solution
A rod of mass m and length 2 R is fixed along te diameter of a ring of same mass m and radius R as shown in figure. The combined body is rolling without slipping along x-axis find the angular momentum about z-axis.
View Solution
A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View SolutionAs shown in the figure, a disc of mass m is rolling without slipping with angular velocity ω. When it crosses point B disc will be in

View Solution
