A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank is
F2
F4
F3
2F3
The correct Answer is:B
F−f=ma1………..(1)
f=ma2……..(2)
α=τI=fR12mR2=2fmR……….(3)
a1−Rα=a2…………(4)
Solving these four equations, we get a1=3F4m,a2=F4m,f=F4,α=F2mR

Similar Questions
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
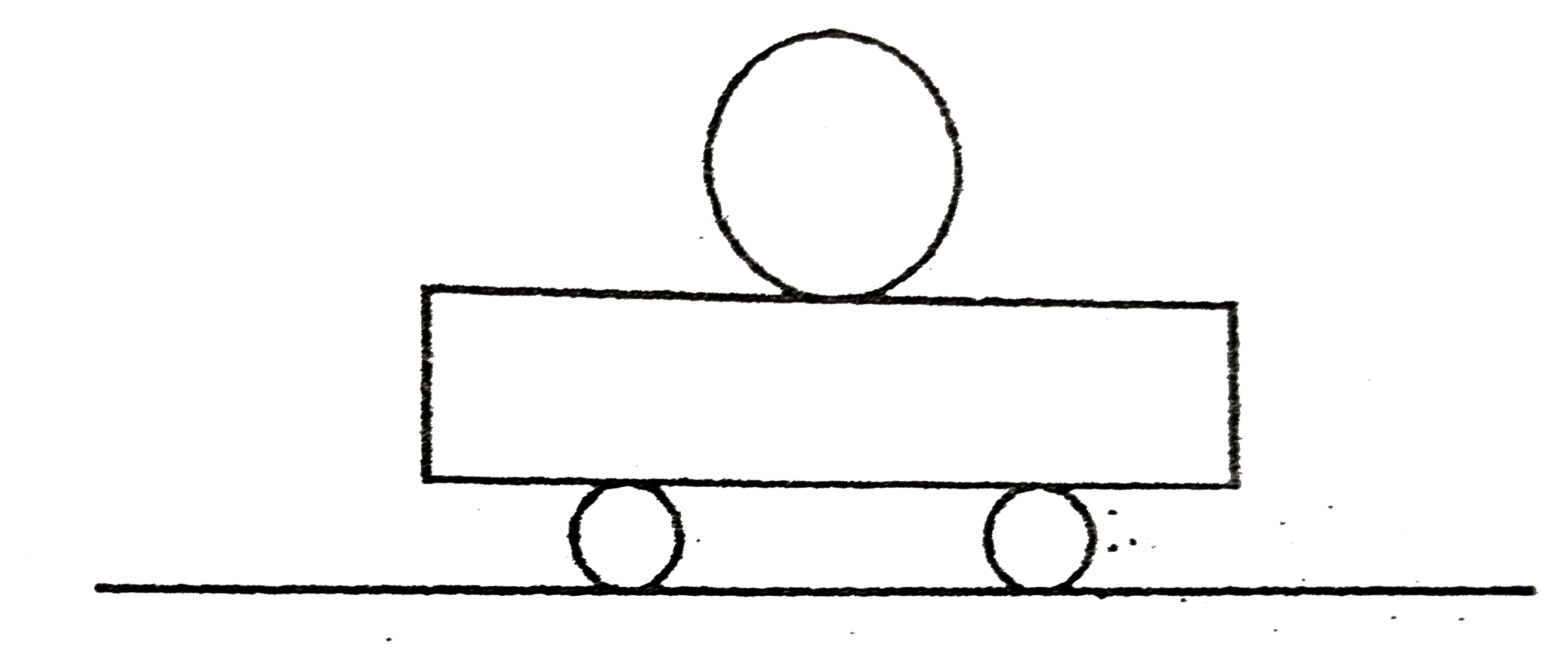
Angular acceleration of sphere is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
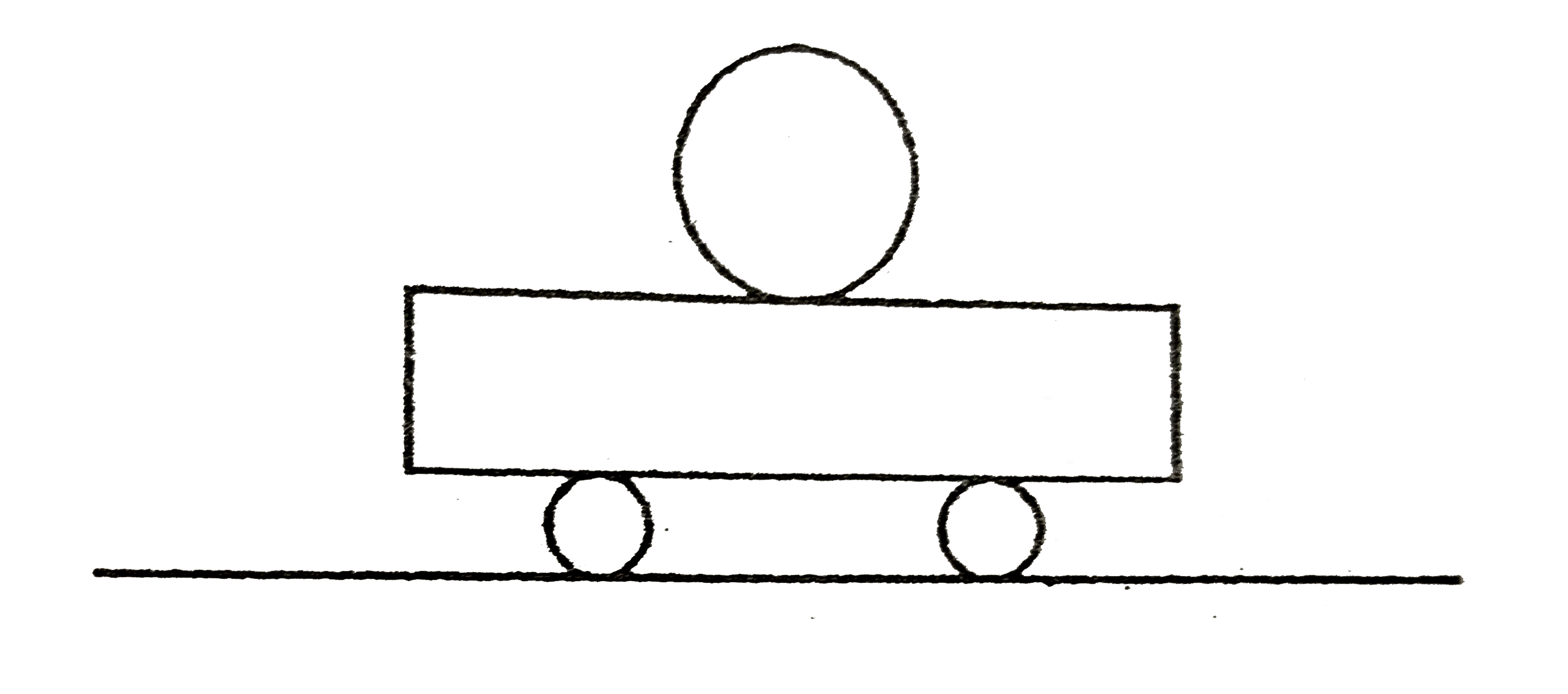
Acceleration of centre of mass of sphere is
View Solution
Knowledge Check
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank isAF2mB3F4mCF4mD3F2mConsider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Acceleration of the plank isA3F16mB11F8mC9F4mDZeroConsider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Friction force acting between the sphere and the plank isAF8B3F8C5F8D7F8
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

When a horizontal force F is applied at centre of sphere, acceleration of the plank is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

Force of friction between sphere and plank is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

A Horizontal force F is applied on the plank. What is the maximum value of F, if μ is coefficient of friction between sphere movment and plank and there is no slipping ?
View SolutionA force F is applied at the centre of a disc of mass M. The minimum value of coefficient of friction of the surface for rolling is
View SolutionA uniform disc of mass m and radius R is free to rotate about its fixed horizontal axis without friction. There is sufficient friction between the inextensible light string and disc to prevent slipping of string over disc. At the shown instant extension in light spring is 3mgK, where m is mass of block, g is acceleration due to gravity and K is spring constant. Then select the correct alternative(s).
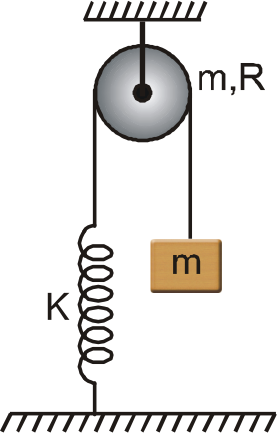
View Solution
