In each situation of Table-1, a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface as shown. At, t=0 (initially) the angular velocity of disc is ω0 and velocity of centre of mass of disc is v0 (in horizontal direction). The relation between v0 and ω0 for each situation and also initial sense of rotation is given in Table-1 . Then match the statements in Table-1 with the corresponding results in Table-2.

[A-P, Q,R, B-p,Q,R, C-P, Q: D-P, Q,R]
In such situation if body is kept in forward or backward slip conditions, maximum friction acts at bottommost point in the opposite direction of slip. Torque of this friction about bottommost point (here A) is zero. Therefore angular momentum about A will remain constant. Further, some part of kinetic energy is lost till slipping continues. Once pure rolling starts (due to friction) kinetic energy becomes constant
Similar Questions
In each situation of column -I a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface as shown At t=0 (initially)the angular velocity of disc is omega_(0) and velocity of centre of mass of disc is v_(0) (in horizontal direction). The relation between v_(0) and ω0 and the initial sense of rotation is given for each situation in column-I then match the statement in column-I with the corresponding results in column-II.

View SolutionA disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :

View Solution
Knowledge Check
A point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
 A(2u3R)B(3u3R)C(5u3R)D(2u5R)
A(2u3R)B(3u3R)C(5u3R)D(2u5R)A uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
ADuring motion , NgtmgBDuring motion, normal reactions acts on the center of massCduring motion, the normal reaction shifts towards positive x-axis from the center of massDduring motion, normal reaction shifts in the direction of the force of friction.A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:
 A3v22gB4v24gCv24gDv22g
A3v22gB4v24gCv24gDv22g
A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : the centre of mass
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be :-
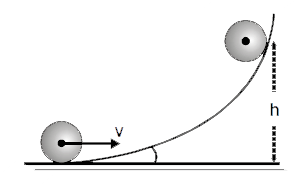
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA disc of mass 2 kg is rolling on a horizontal surface without slipping with a velocity of 0.1 m/s. What is its rotational kinetic energy?
View Solution
