A heater is designed to operate with a power of in a line. It is connected in combination with a resistance of and a resistance , to a mains as shown in figure. What will be the value of so that the heater operates with a power of ?
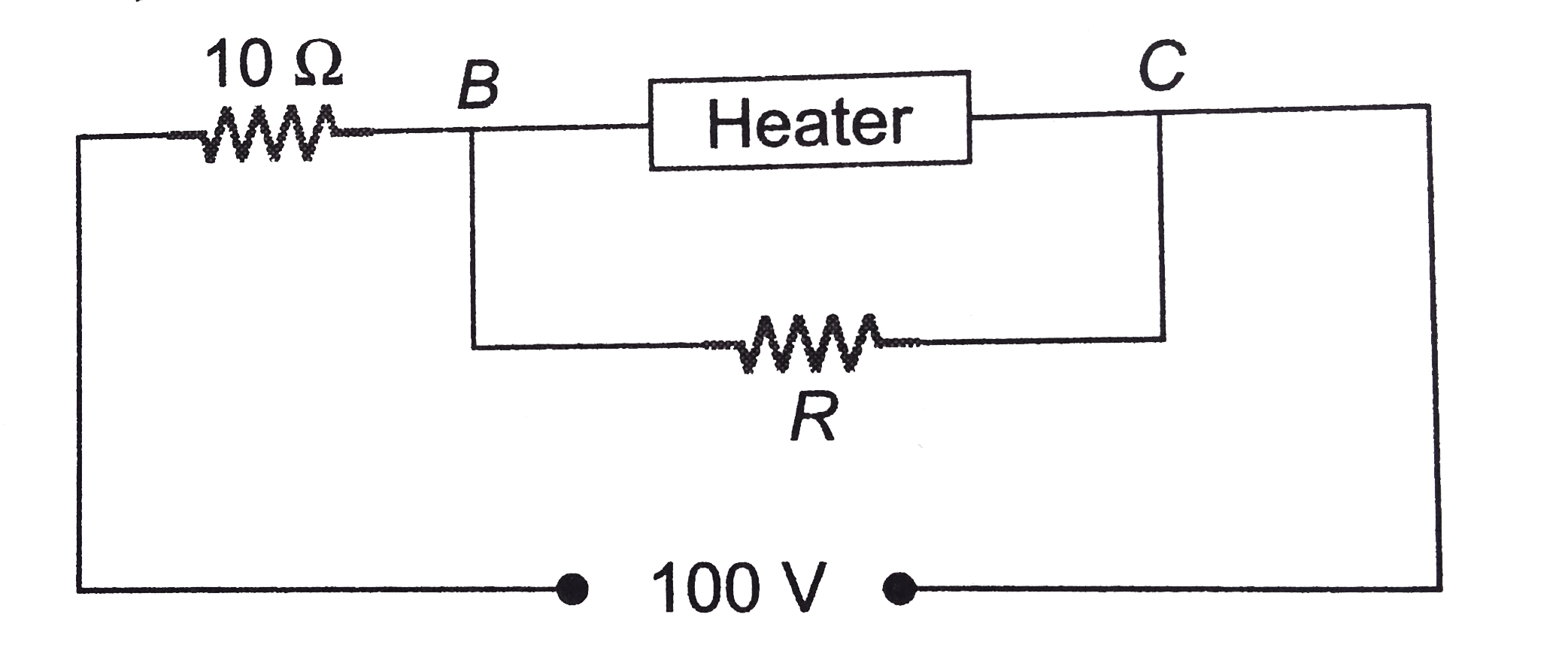
From , Resistance of heater ,
From Current required across heater for power of 62.5W
, Main current in the circuit
This current will distribute in inverse ratio of resistance between heater and R.
SOlving this equation we get
Similar Questions
A heater is designed to operate with a power of 1000W in a 100V line. It is connected in combination with a resistace of 10Ω and a resitance. R, to a 100V mains, as shown in Fig. 6.6 What should be the value of R so that the heat operates with a power of 62.5 W ?
View SolutionA heater is designed to operate with a power of 1000 walts in a 100 volt line. It is connected in a combinations with a resistance of 10 ohms and a resistance R to a 100 volts mains as shown in figure. What should be the value of R so that the heater operates with a power of 62.5 watts.
 .
.
View Solution
Knowledge Check
An ac source is connected across a resistance of 10Ω The power dissipated in the resistor is 100W The rms valuse of the current and voltge are .
A√10A,√1000VB2√10A,2√1000VC2√10A,2√1000VD√10A,2√1000VAn AC generator of 220 V having internal resistance r=10Ω and external resistance R=100Ω. What is the power developed in the external circuit?
A484 WB400 WC441 WD369 WA 100V voltmeter having an internal resistance of 20kΩ is connected in series with a large resistance R across a 110V line. What is the magnitude of resistance R if the voltmeter reads 5V?
A210kΩB315kΩC420kΩD440kΩ
If two buibs of 25 W and 100 W rated at 400 V are connected in series across a440 V supply, will both the bulb fuse? If not, then which one ?
(b) Two bulbs rated at 60 W and 100 W (220 V) are connected (i) in series and (ii) in parallel. Find the heat dissipated in the bulbs and also the total heat dissipatedin the circuit.
(c) A heater is designed to operate with a power of1000 watts in a 100 volt line. It is connected with an identical heater (B) in series and a100 V second heater (C) in parallel as shown. What should be the resistance of C so that the heater A may operate at a power level of 62.5 watts, if the entire combination is connected across a 100 V line
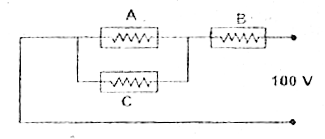
View SolutionAn electric heater is designed to operate in 100V main with a power output of 1000W .When it is connected to a 25V source,power output is:
View SolutionA 100V voltmeter having an internal resistance of 20kΩ is connected in series with a large resistance R across a 110V line. What is the magnitude of resistance R if the voltmeter reads 5V?
View SolutionTwo electric bulbs, each designed to operate with a power of 500W in 220V line, are in series with a 100V line. What will be the power generated by each bulb?
View SolutionA potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and of of 40cm of the potentiometer wire. What is the value of R?
View Solution