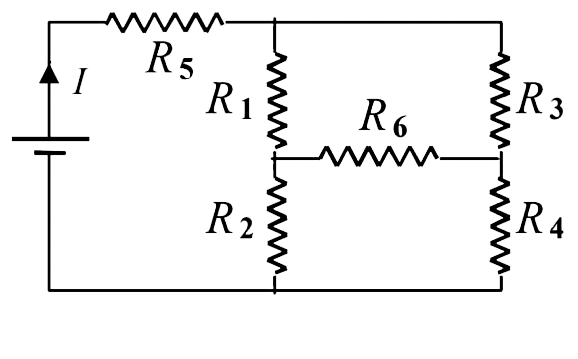
In the given circuit, it is observed that the current I is independent of the value of the resistance R6. Then the resistance values must satisfy
 .
.
A
R1R2R5=R3R4R6
B
1R5+1R6=1R1+R2+1R3+R4
C
R1R4=R2R3
D
R1R3=R2R4=R5R6
Video Solution
Text Solution
Since current I is independent of R6 it follows that the resistance R1,R2,R3andR4 must form a balanced Wheatstone bridge.
|
Similar Questions
Knowledge Check
In the given circuit, it is observed that the current I is independent of the value of the resistance R6. Then the resistance values must satisfy
 .A1R5+1R6=1R1+R2.1R3+R4BR1R4=R2R3CR1R2R5=R3R4R6DR1R3=R2R4=R5R6
.A1R5+1R6=1R1+R2.1R3+R4BR1R4=R2R3CR1R2R5=R3R4R6DR1R3=R2R4=R5R6In the circuit shown below, the ammeter reading is zero. Then, the value of the resistance R is
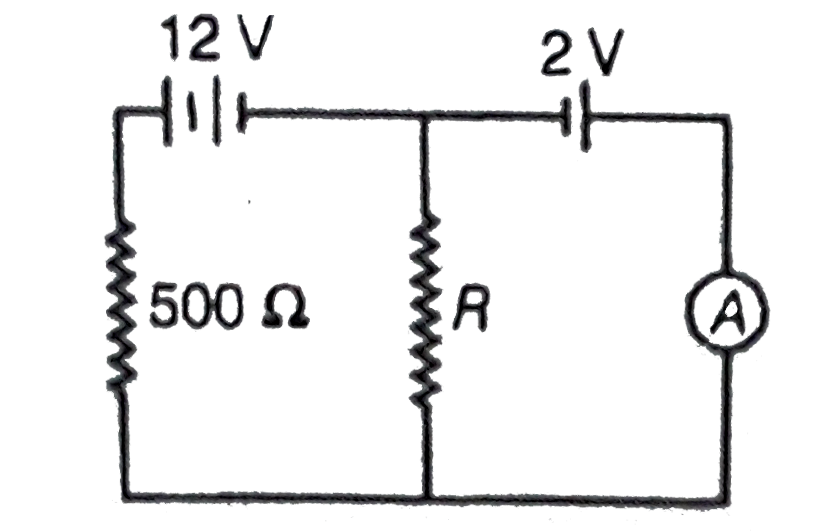 A50ΩB100ΩC200ΩD400Ω
A50ΩB100ΩC200ΩD400ΩIn the circuit shown below, the ammeter reading is zero. Then, the value of the resistance R is
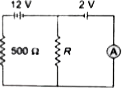 A50ΩB100ΩC200ΩD400Ω
A50ΩB100ΩC200ΩD400Ω
In the given circuit,find the current through 6Ω resistance

View Solution
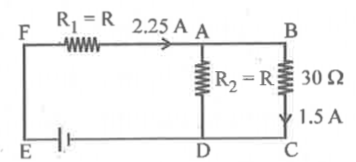
In the given circuit, the current in each resistance is:
View SolutionThe value of the current I in the given circuit is
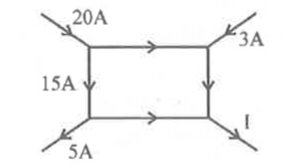
View SolutionIn the given circuit the current is to be measured the value of the current if the ammeter shown is a galvanometer with a resistance Rg=60ω is

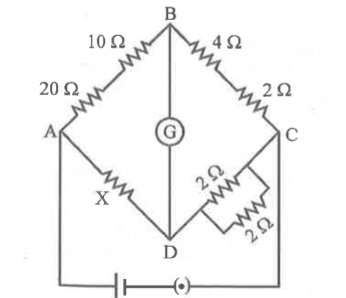
View SolutionIn the given circuit, the resistances are given in ohm. The current through the 10Ω resistance is 3 A while that through the resistance X is 1 A. No current passes through the galavanometer. The values of the unknown resistances X and Y are respectively (in ohm)
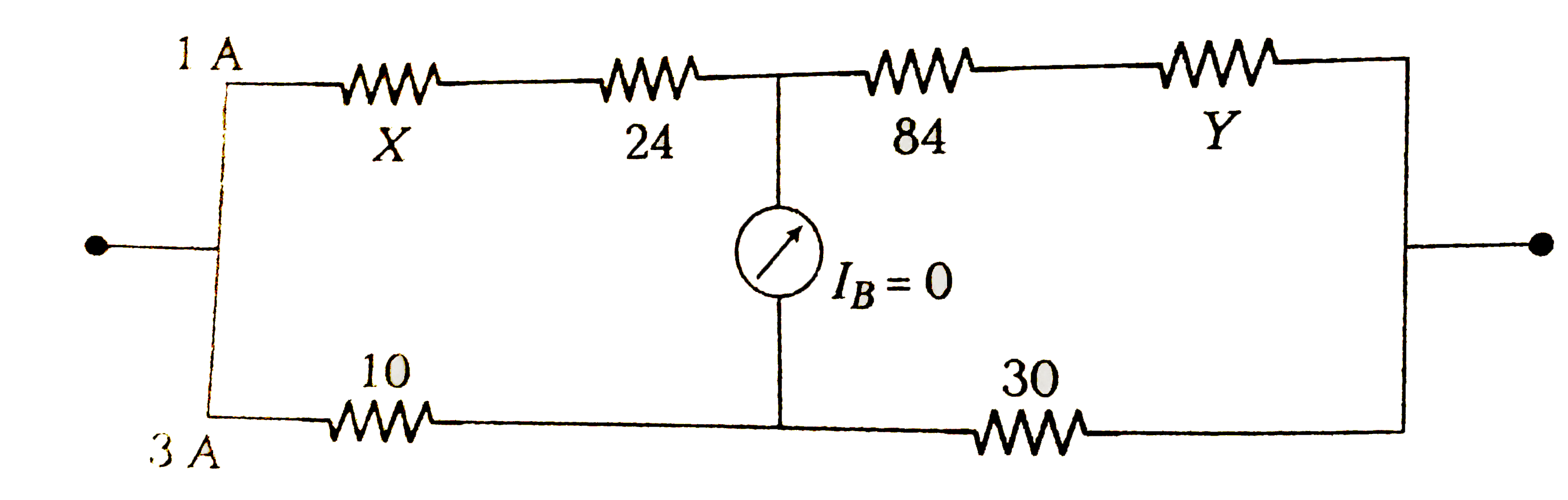
View Solution