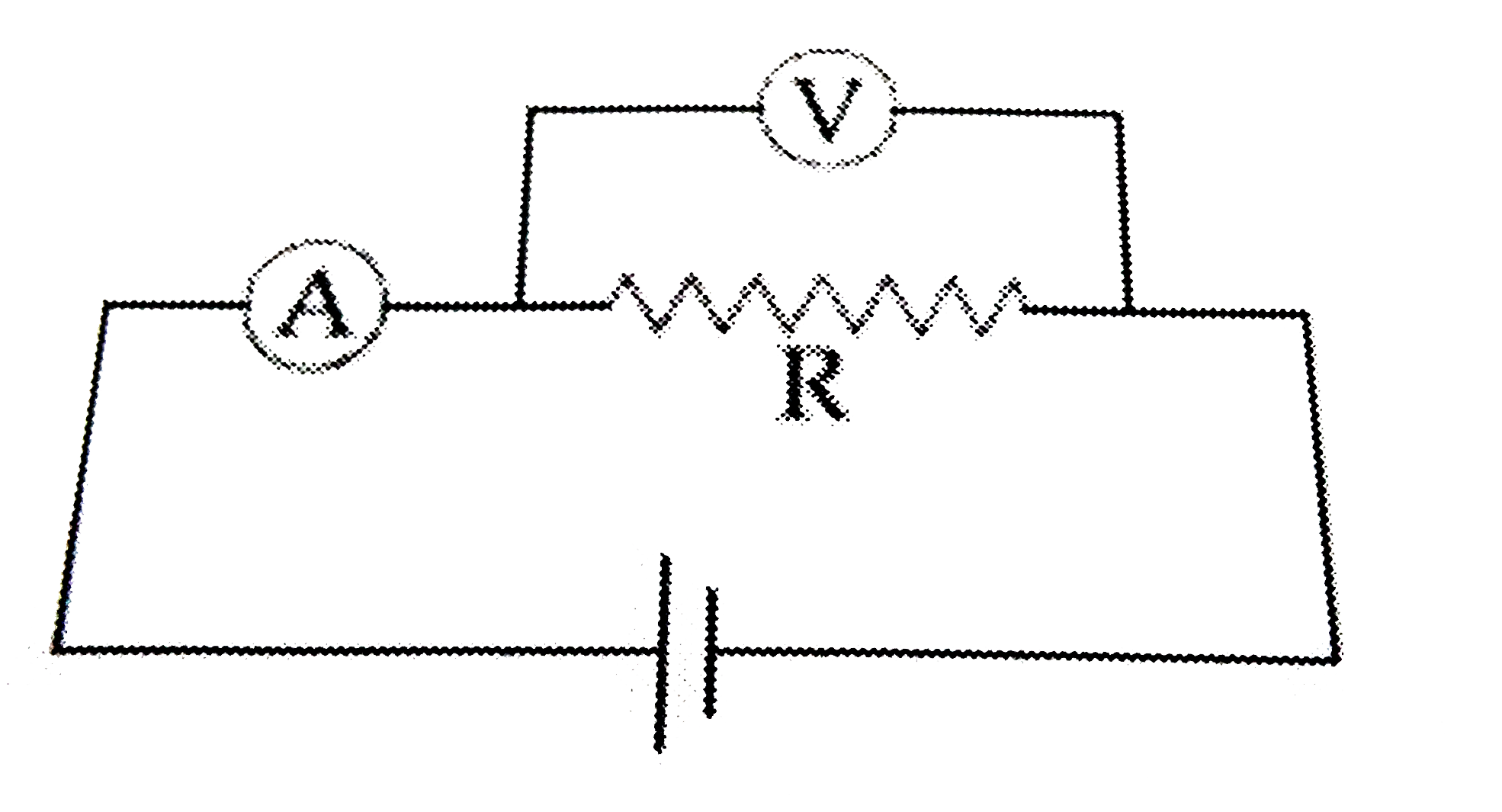
The actual value of resistance R, shown in the figure is 30Ω. This is measured in an experiment as shown using the standard formula R=VI, where V and I are the readings of the voltmeter and ammeter, respectively. If the measured value of R is 5% less, then the internal resistance of the voltmeter is
600Ω
350Ω
35Ω
570
Vm=Rmjm=jR.R
⇒Rm=jR×Rjm=R(rR+r)
⇒1Rm=(R+r)Rr=1r+1R⇒1r=1Rm−1R=195R−1R=1R×595⇒r=30×955=570Ω
Similar Questions
Determine the resistance r if an ammeter shows a current of I=5A and a voltmeter 100V. The internal resistance of the voltmeter is R=2,500Ω
View SolutionConsider the two circuits P and Q, shown below, which are used 20 measure the unknown resistance R.
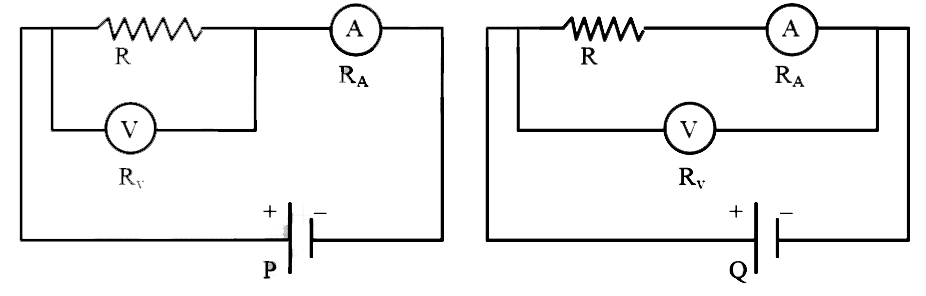
In each case, the resistance is estimated by using Ohm's law Rest=V/I, Where V and I are the readings of the voltmeter and the ammeter respectively. The meter resistances, Rv and RA are such that RA<<R<<Rv. The internal resistance of the battery may be ignored. The absolute error in the estimate of the resistance is denoted by δR=|R=Rest|.
View Solution
Knowledge Check
For the adjoining circuit diagram, the readings of ammeter and voltmeter are 2A and 120 V respectively. If the value of R is 75Ω, then the voltmeter resistance will be
 A100ΩB150ΩC300ΩD75Ω
A100ΩB150ΩC300ΩD75ΩIn the adjoining circuit diagram, the readings of ammeter and voltmeter are 2 A and 120 V, respectively. If the value of R is 75Ω, then the voltmeter resistance will be
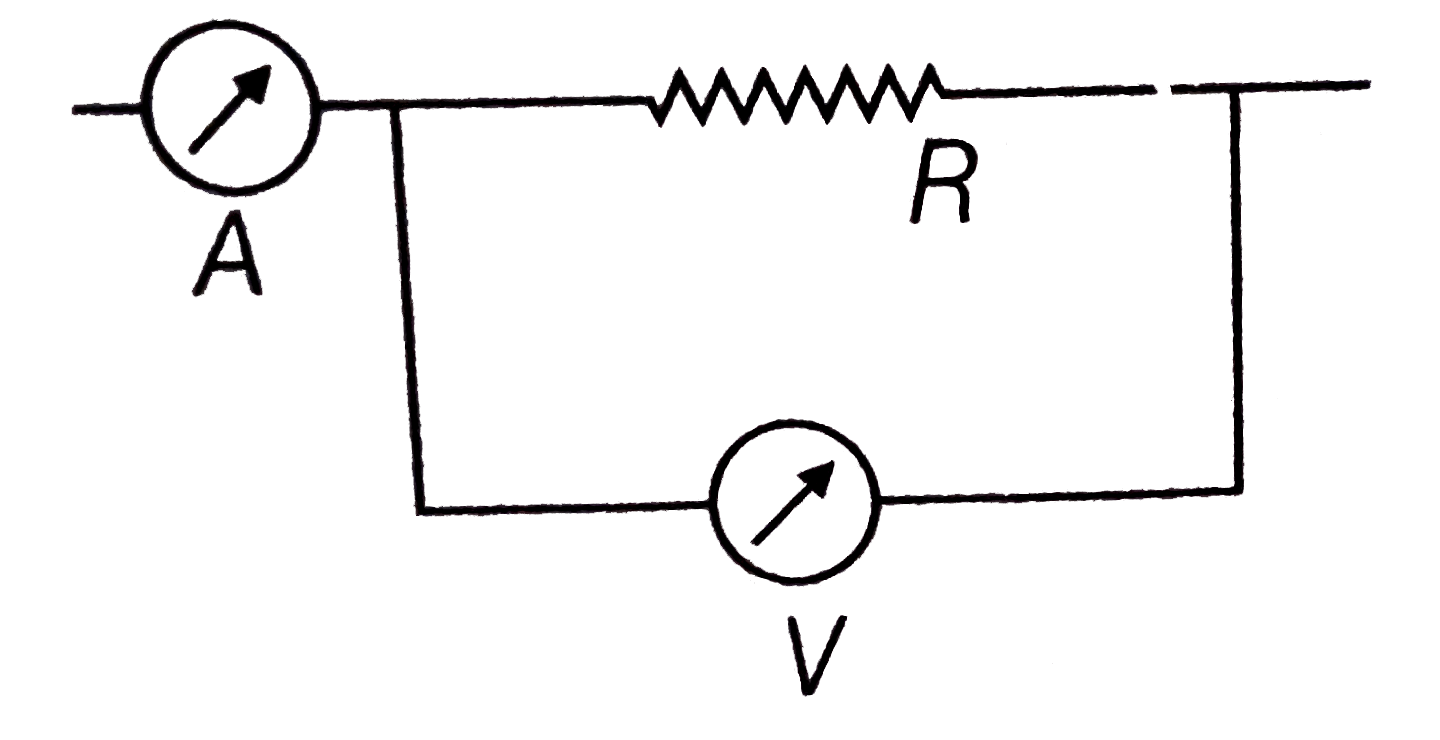 A100ΩB150ΩC300ΩD75Ω
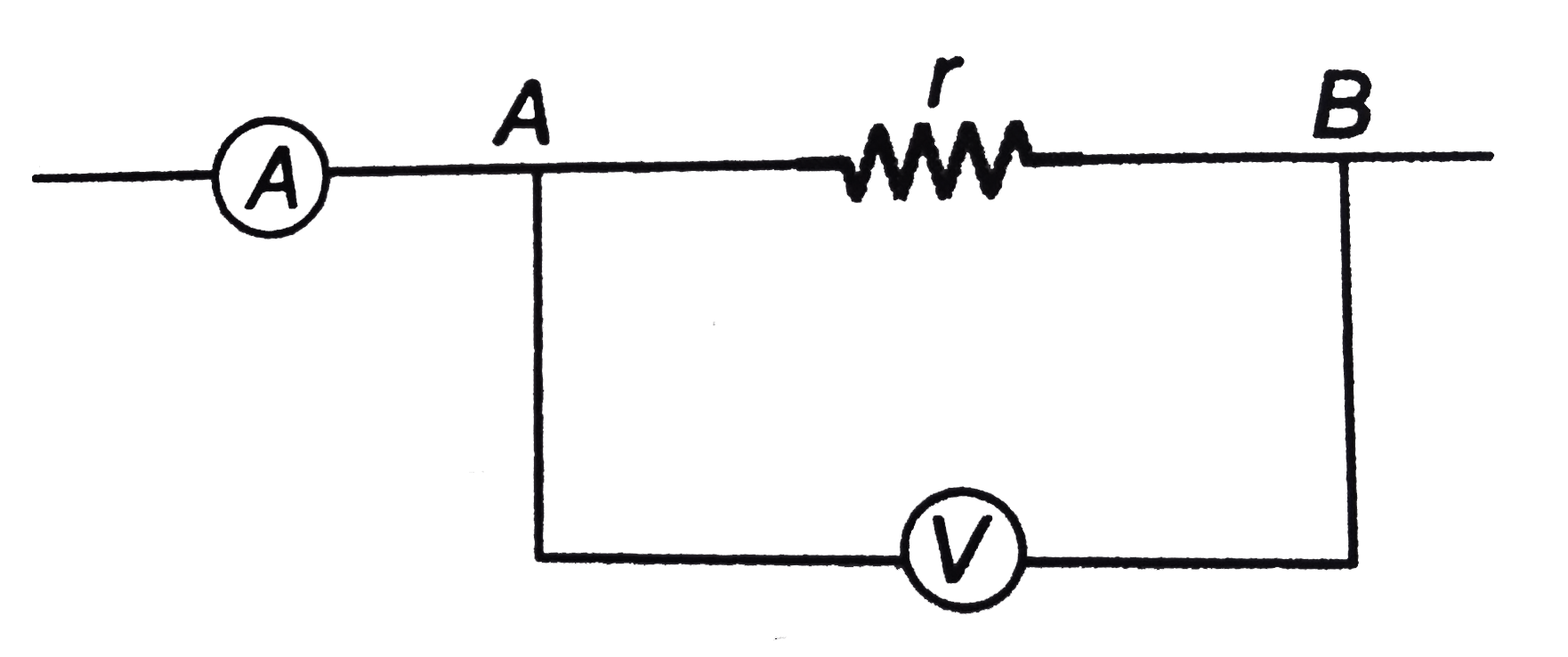
A100ΩB150ΩC300ΩD75ΩLet V and I be the readings of the voltmeter and the ammeter respectively as shown in the figure. Let RV and RA be their corresponding resistancce Therefore,
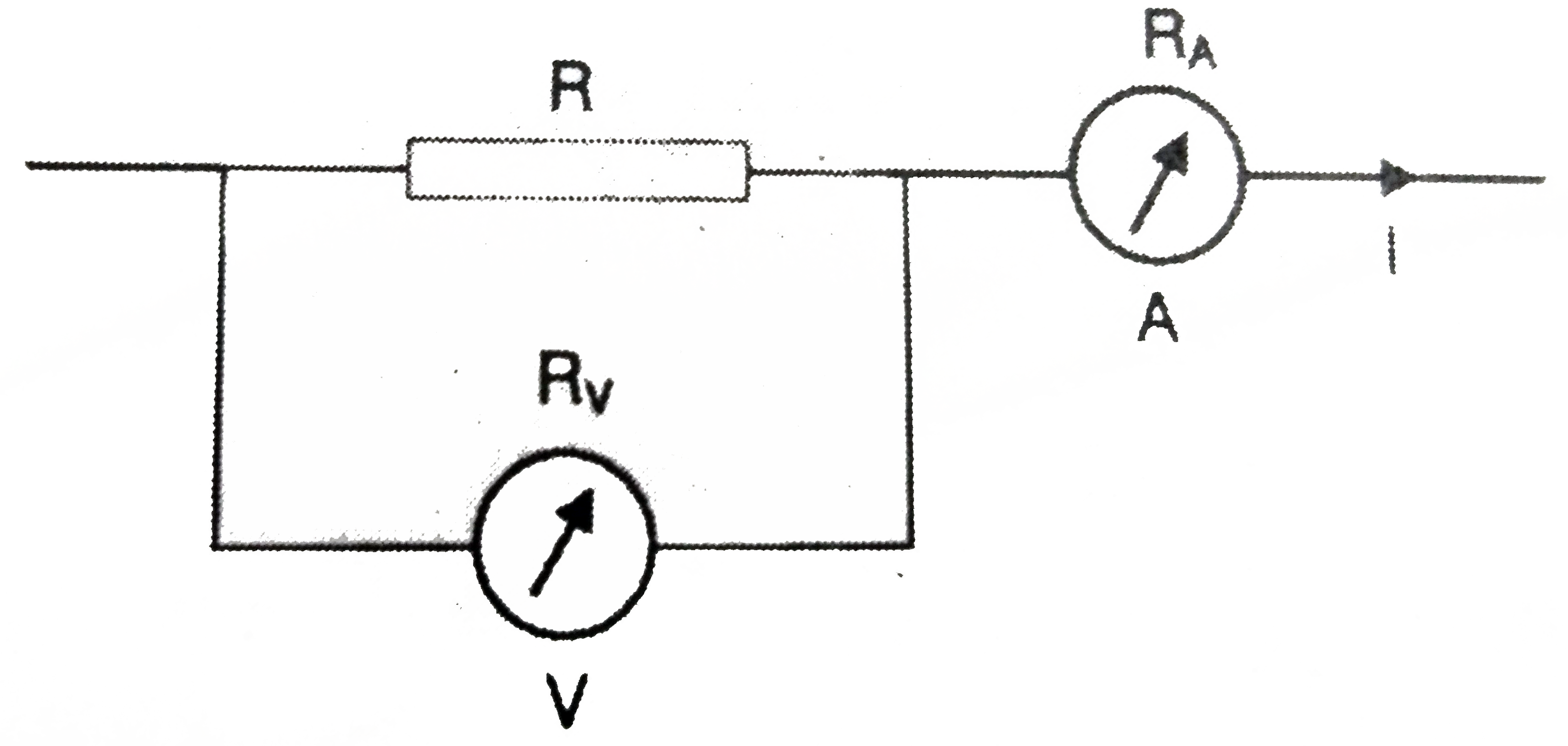 AR=VIBR=VI−(VRV)CR=RV−RADR=V(R+RA)IRA
AR=VIBR=VI−(VRV)CR=RV−RADR=V(R+RA)IRA
Resistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRGrespectively ) are finite and non zero.

Let RvandRG be the calculated values in the two cases A and B respectively.
If the resistance of voltmeter is Rv=1kΩ and that of ammeter is RG=1Ω the magnitude of the percentage error in the measurement of R (the value of R is nearly 10Ω ) is:
View SolutionThe ammeter A reads 2A and the voltmeter V reads 20V, the value of resistance R is (Assuming finite resistance's of ammeter and voltmeter)
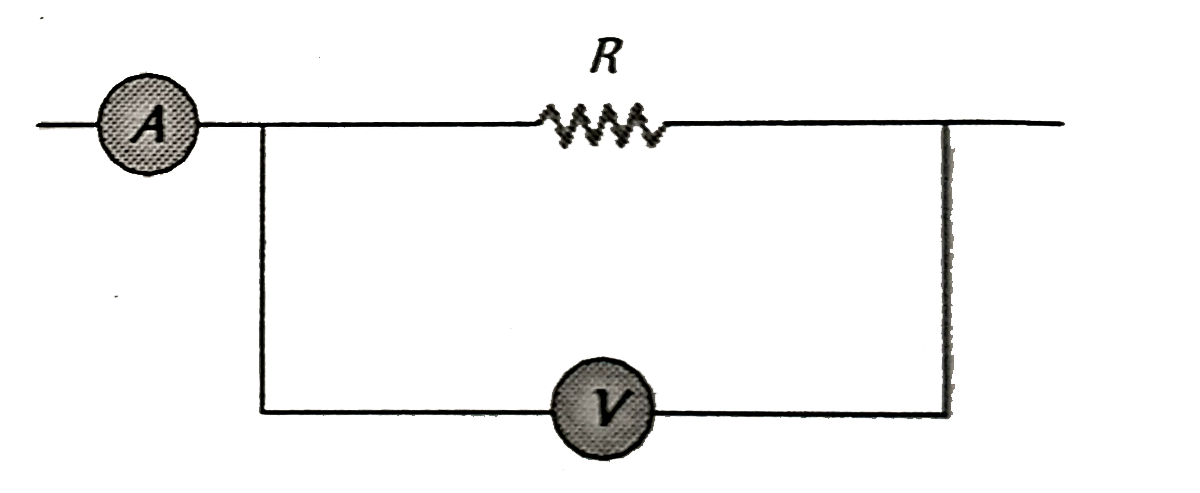
View SolutionResistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRGrespectively ) are finite and non zero.
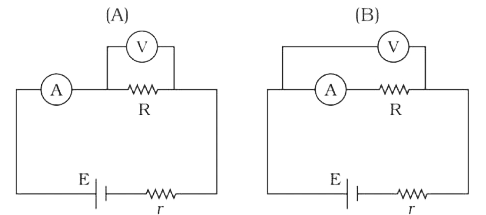
Let RvandRG be the calculated values in the two cases A and B respectively.
The relation between RBand the actual value of R is:
View SolutionThe value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
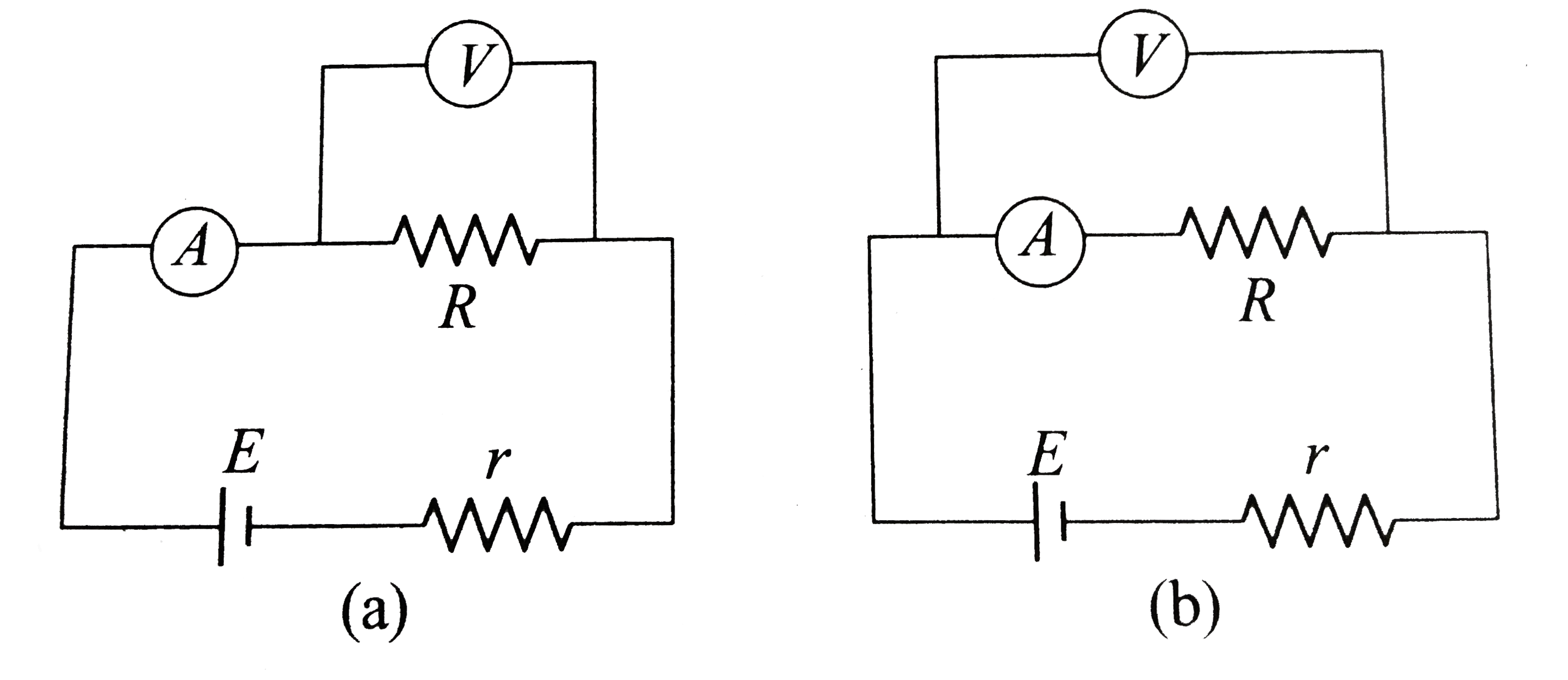 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is RV=1kΩ and the percentage error in the measurement of R (the value of R is nearly 10Ω)is
View SolutionThe value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
The relation between RA and the actual value of R is
View Solution
