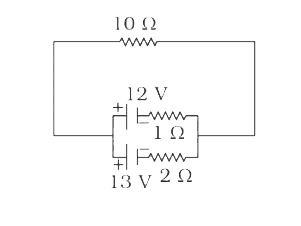
Two batteries with e.m.f 12 V and 13 V are connected in parallel across a load resistor of 10Ω. The internal resistances of the two batteries are 1Ω and 2Ω respectively. The voltage across the load lies between :
11.6 V and 11.7 V
11.5 V and 11.6 V
11.4 V and 11.5 V
11.7 V and 11.8 V
For parallel combination of cells,
Eeq=E1r1+E2r21r1+1r2∴Eeq=121+13212+12=373V
Potential drop across 10Ω resistance
V=(EReq)×10=37/3(10+23)×10=11.56V
Alternative method
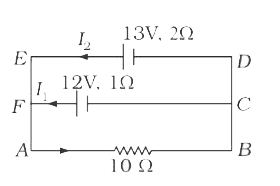
Applying KVL in loop ABCFA,−12+10(I1+I2)+1×I1=0
⇒12=11I1+10I2 .......(i)
Similarly in loop ABDEA, −13+10(I1+I2)+2×I2=0
⇒12=10I1+12I2..........(ii)
SOlving Eqs (i) and (ii) we get I1=716A,I2=2332A
∴ VOltage drop across 10Ω resistance is V=10(716+2332)=11.56V
Similar Questions
The series combination of two batteries, both of the same emf 10 V, but different internal resistance of 10Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 10Ω is zero, the value of R (in Ω ) is : _________.
View SolutionThe series combination of two batteries both of the same emf 10 V, but different internal resistance of 20Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 20Ω is zero, the value of R(in Ω) is __________.
View Solution
Knowledge Check
Two batteries with emf 12V and 13V are connected in parallel across a load resistor of 10Ω. The internal resistances of the two batteries are 1Ωand2Ω respectively. The voltage across the load lies between
A11.4V and 11.5VB11.7 V and 11.8VC11.6V and 11.7VD11.5 V and 11.6V4 cells each of emf 2 V and internal resistance of 1Ω are connected in parallel to a load resistor of 2Ω. Then the current through the load resistor is
A2AB1.5AC1AD0.888AThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
A1.95VB1.90VC0.50VD2.00V
The cell has an emf of 2 V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
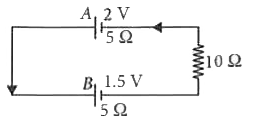
View SolutionTwo cells A and B of e.m.f.2 V and 1.5 V respectively, are connected as shown in figure through an external resistance 10 Ω The internal resistance of each cell is 5 Ω. The potential difference EAandEB across the terminals of the cells A and B respectively are
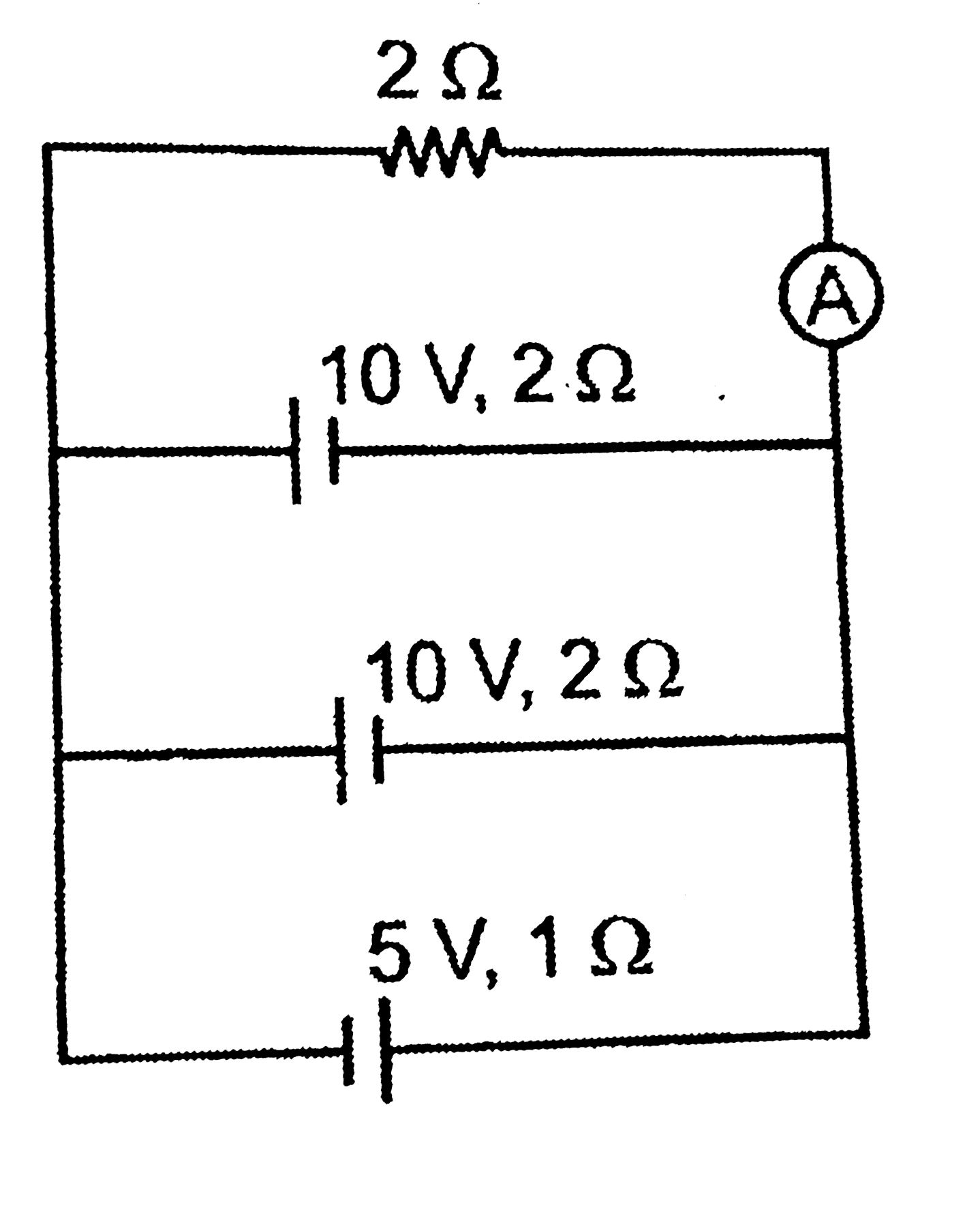
View SolutionThree batteries having emfs and internal resistances as shown in figure are connected across a resistor of 2Ω. The reading of ammeter is
View SolutionA cell of emf 2.0 V and internal resistance 0.1 Ω is connected with a resistance of 3.9Ω. The voltage across the cell terminals will be
View Solution