A Wheatstone network consists of four resistances (in cyclic order) 10Ω,5Ω,6Ω,6Ω . The resistance that must be connected across the 10Ωresistance so that the network becomes balanced is (in Ohm):
10
5
20
6
To solve the problem of finding the resistance that must be connected across the 10Ω resistance in a Wheatstone bridge to achieve balance, we can follow these steps:
1. Identify the Resistor Values:
The Wheatstone network consists of four resistances in cyclic order:
- P = 10Ω
- Q = 5Ω
- R = 6Ω
- S = 6Ω
2. Understand the Balance Condition:
For a Wheatstone bridge to be balanced, the ratio of the resistances must satisfy the equation:
\(
\frac{P}{Q} = \frac{R}{S}
\)
Here, we need to find the value of resistance \( P' \) that we will connect across the 10Ω resistor.
3. Set Up the Equation:
Let the resistance we need to connect across the 10Ω resistor be \( R' \). The new effective resistance \( P \) will then be in parallel with \( R' \):
\(
P = \frac{R' \cdot 10Ω}{R' + 10Ω}
\)
We want this effective resistance \( P \) to equal 5Ω (the value of Q).
4. Set Up the Equation for Balance:
From the balance condition:
\(
\frac{P}{Q} = \frac{R}{S} \implies \frac{\frac{R' \cdot 10Ω}{R' + 10Ω}}{5Ω} = \frac{6Ω}{6Ω}
\)
This simplifies to:
\(
\frac{R' \cdot 10Ω}{R' + 10Ω} = 5Ω
\)
5. Cross Multiply to Solve for \( R' \):
Cross multiplying gives:
\(
R' \cdot 10Ω = 5Ω(R' + 10Ω)
\)
Expanding the right side:
\(
10R' = 5R' + 50
\)
6. Rearranging the Equation:
Rearranging gives:
\(
10R' - 5R' = 50 \implies 5R' = 50
\)
7. Solve for \( R' \):
Dividing both sides by 5:
\(
R' = 10Ω
\)
Final Answer:
The resistance that must be connected across the 10Ω resistance to balance the Wheatstone bridge is 10Ω.
The Wheatstone network consists of four resistances in cyclic order:
- P = 10Ω
- Q = 5Ω
- R = 6Ω
- S = 6Ω
For a Wheatstone bridge to be balanced, the ratio of the resistances must satisfy the equation:
\(
\frac{P}{Q} = \frac{R}{S}
\)
Here, we need to find the value of resistance \( P' \) that we will connect across the 10Ω resistor.
Let the resistance we need to connect across the 10Ω resistor be \( R' \). The new effective resistance \( P \) will then be in parallel with \( R' \):
\(
P = \frac{R' \cdot 10Ω}{R' + 10Ω}
\)
We want this effective resistance \( P \) to equal 5Ω (the value of Q).
From the balance condition:
\(
\frac{P}{Q} = \frac{R}{S} \implies \frac{\frac{R' \cdot 10Ω}{R' + 10Ω}}{5Ω} = \frac{6Ω}{6Ω}
\)
This simplifies to:
\(
\frac{R' \cdot 10Ω}{R' + 10Ω} = 5Ω
\)
Cross multiplying gives:
\(
R' \cdot 10Ω = 5Ω(R' + 10Ω)
\)
Expanding the right side:
\(
10R' = 5R' + 50
\)
Rearranging gives:
\(
10R' - 5R' = 50 \implies 5R' = 50
\)
Dividing both sides by 5:
\(
R' = 10Ω
\)
The resistance that must be connected across the 10Ω resistance to balance the Wheatstone bridge is 10Ω.
Similar Questions
Four resistances 6Ω,6Ω,6Ω and 18Ω form a Wheatstone bridge. Find the resistance which connected across the 18Ω resistance will balance the network.
View SolutionIn a typical wheatstone network the resistance in cyclic order are A=10Ω,B=5O,ega,C=4Ω and D=4Ω for the bridge to be balanced.

View Solution
Knowledge Check
For resistances arranged to form a wheatstone's network are 10Ω,15Ω,6Ωand36Ω. What resistance should be connected across the 36Ω resistance to balance the bridge ?
A9ΩB12ΩC15ΩD18ΩFour resistances arranged to form a Wheatstone's network are 8Ω,12Ω,6Ω, and 27Ω. The resistance that should be connected across 27Ω resistance to balance the bridge is
A13.5ΩB15.5ΩC27ΩD12ΩIn a typical Wheatstone network, the resistances in cyclic order are A=10Ω,B=5Ω,C=4Ω D=4Ω for the bridge to be balanced
 A10Ω should be connected in parallel with AB10Ω should be connected in series with AC5Ω should be connected in series with BD5Ω should be connected in parallel with B
A10Ω should be connected in parallel with AB10Ω should be connected in series with AC5Ω should be connected in series with BD5Ω should be connected in parallel with B
Four resistances 5Ω,5Ω,8Ω and 10Ω form a Wheatstone network. Find the resistance whch connected across the 10Ω resistance will balance the network.
View SolutionIn Wheatstone bridge, the resistances in four arms are 10Ω,10Ω,10Ω and 20Ω. To make the bridge balance, resistance connected across 20Ω is
View SolutionWhat is the current in 10Ω resistance in the following network ?
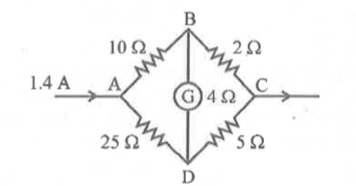
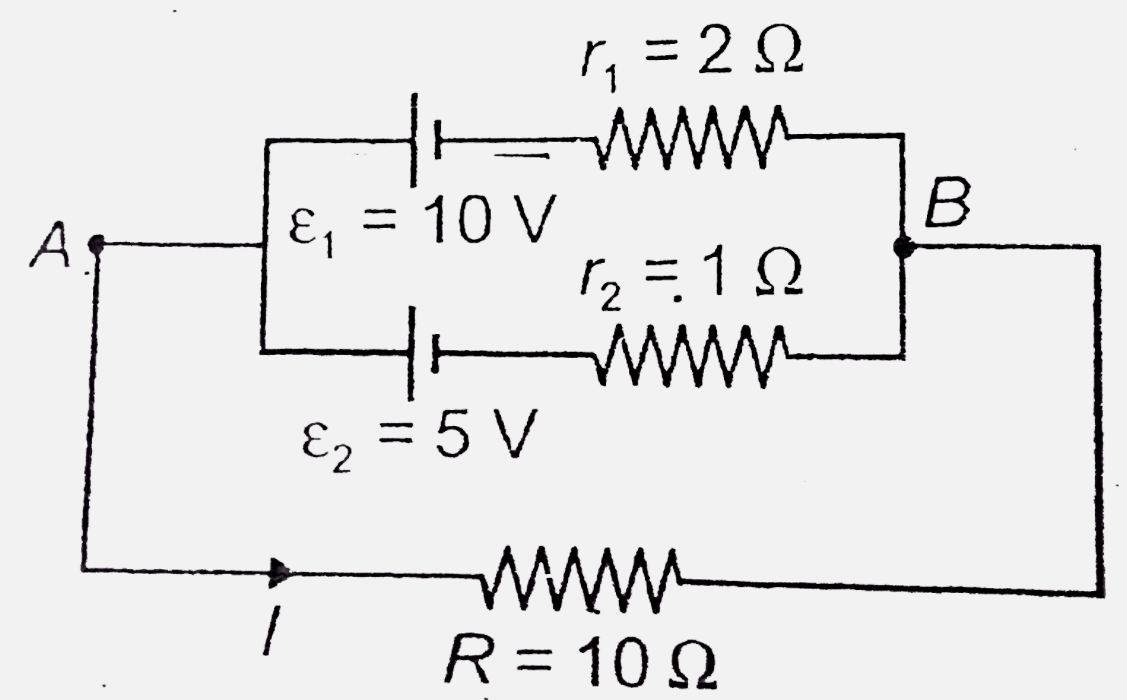
View SolutionFind the current l through then 10Ω resistance in the network shown in figure.
View SolutionIn a typical Wheatstone's network, the resistances in the cyclic order are P=10Ω,Q=5Ω,S=4ΩandR=4Ω. For balancing the bridge, a resistance of
View Solution

