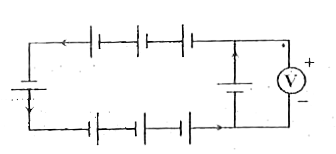
Voltmeters V1andV2 are placed in series and then connected to an ideal battery. V1 reads 80 V and has resistance 20KΩ and V2 has resistance 10KΩ . The EMF of the battery is:
240V
220V
160V
120V
To find the EMF of the battery when voltmeters V1 and V2 are connected in series, we can follow these steps:
Step 1: Identify Given Values
- Reading of voltmeter V1=80V
- Resistance of V1=20kΩ=20×103Ω
- Resistance of V2=10kΩ=10×103Ω
Step 2: Understand the Circuit
The voltmeters are connected in series to an ideal battery. The total EMF of the battery (E) is the sum of the voltages across both voltmeters.
Step 3: Write the Equation for EMF
The EMF of the battery can be expressed as:
E=V1+V2
Where V2 is the voltage across voltmeter V2.
Step 4: Calculate the Current in the Circuit
Let I be the current flowing through the circuit. The voltage across V1 can be calculated using Ohm's Law:
V1=I×R1
Where R1=20kΩ.
Substituting the known values:
80=I×(20×103)
Solving for I:
I=8020×103=8020000=4×10−3A
Step 5: Calculate Voltage Across V2
Now, we can find the voltage across V2 using Ohm's Law again:
V2=I×R2
Where R2=10kΩ.
Substituting the values:
V2=(4×10−3)×(10×103)=4×10−3×10000=40V
Step 6: Calculate the EMF of the Battery
Now, substitute V1 and V2 back into the equation for EMF:
E=V1+V2=80+40=120V
Final Answer
The EMF of the battery is:
120V
- Reading of voltmeter V1=80V
- Resistance of V1=20kΩ=20×103Ω
- Resistance of V2=10kΩ=10×103Ω
The voltmeters are connected in series to an ideal battery. The total EMF of the battery (E) is the sum of the voltages across both voltmeters.
The EMF of the battery can be expressed as:
E=V1+V2
Where V2 is the voltage across voltmeter V2.
Let I be the current flowing through the circuit. The voltage across V1 can be calculated using Ohm's Law:
V1=I×R1
Where R1=20kΩ.
80=I×(20×103)
Solving for I:
I=8020×103=8020000=4×10−3A
Now, we can find the voltage across V2 using Ohm's Law again:
V2=I×R2
Where R2=10kΩ.
V2=(4×10−3)×(10×103)=4×10−3×10000=40V
Now, substitute V1 and V2 back into the equation for EMF:
E=V1+V2=80+40=120V
The EMF of the battery is:
120V
Similar Questions
Knowledge Check
Voltmeters V1 and V2 are connected in series across a D.C. line V1 reads 80 volts and has a per volt resistance of 200ohms, V2 has a total resistance of 32 kilo ohms.
The line voltage isA120 voltsB160 voltsC220 voltsD240 voltsAn ideal voltmeter of 1 V has the resistance equal to
AzeroBinfiniteCuinityDNone of theseAn ammeter and a voltmeter are connected in series to an ideal battery of emf E. If the ammeter reads I and voltmeter reading V, then
AV<εBthe resistance of voltmeter is V/ICP.D. across the ammeter is E-VDAmmeter and voltmeter have equivalent resistance = E/l
A resistor is connected to a battery of emf 10 V and internal resistance 0.3Ω. What is the resistance of the resistor to be inserted in the circuit for the circuit current 1.2A?
View SolutionA voltmeter of range of 10 V and resistance 5000Ω is connected in series with a battery and a resistor of 500Ω by mistake. If the voltmeter reading is 8V, what is the emf of the battery? (Neglect internal resistance of battery).
View SolutionIn the circuit shown below, each battery is 5 V and has an internal resistance of 0.2Ω.
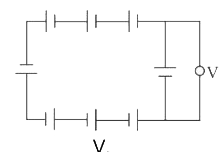
The reading in the ideal voltmeter V is __________V.
View SolutionA voltmeter of resistance 100Ω connected to the terminals of a cell reads 2 V. When the voltmeter is replaced by a resistance 1Ω and an ammeter of 1Ω , the ammeter reads 1 A. The EMF of the cell is __________ V.
View SolutionA voltmeter has a resistance of 50Ω is connected across a cell of e.m.f. 2V and internal resistance 10Ω. The reading of voltmeter is
View Solution