State the condition for maximum current to be drawn from the cell.
To determine the condition for maximum current to be drawn from a cell, we can analyze the relationship between the electromotive force (EMF) of the cell, its internal resistance, and the external resistance connected to it.
1. Understanding the Circuit:
- Consider a cell with an EMF E and an internal resistance r.
- Connect this cell to an external resistor R.
2. Current Calculation:
- The total resistance in the circuit is the sum of the internal resistance and the external resistance, which can be expressed as:
Rtotal=R+r
- According to Ohm's law, the current i flowing through the circuit can be calculated using the formula:
i=ER+r
3. Condition for Maximum Current:
- To find the condition for maximum current, we need to analyze the expression for i.
- The current i is inversely proportional to the total resistance R+r. Therefore, to maximize i, we need to minimize R+r.
- Since the internal resistance r is a constant for a given battery, we can only control the external resistance R.
4. Setting External Resistance to Zero:
- The minimum value of R is 0. Thus, for maximum current, we set:
R=0
- This means that the external circuit should be a short circuit (a wire with negligible resistance).
5. Conclusion:
- The condition for maximum current to be drawn from the cell is when the external resistance R is equal to zero, effectively short-circuiting the cell.
Final Answer:
The condition for maximum current to be drawn from the cell is when the external resistance R is zero (i.e., the circuit is short-circuited).
- Consider a cell with an EMF E and an internal resistance r.
- Connect this cell to an external resistor R.
- The total resistance in the circuit is the sum of the internal resistance and the external resistance, which can be expressed as:
Rtotal=R+r
- According to Ohm's law, the current i flowing through the circuit can be calculated using the formula:
i=ER+r
- To find the condition for maximum current, we need to analyze the expression for i.
- The current i is inversely proportional to the total resistance R+r. Therefore, to maximize i, we need to minimize R+r.
- Since the internal resistance r is a constant for a given battery, we can only control the external resistance R.
- The minimum value of R is 0. Thus, for maximum current, we set:
R=0
- This means that the external circuit should be a short circuit (a wire with negligible resistance).
- The condition for maximum current to be drawn from the cell is when the external resistance R is equal to zero, effectively short-circuiting the cell.
The condition for maximum current to be drawn from the cell is when the external resistance R is zero (i.e., the circuit is short-circuited).
Similar Questions
Knowledge Check
In a circuit a cell with internal resistance r is connected to an external resistance R. The condition for the maximum current that drawn from the cell is
AR=rBR<rCR>rDR=0
Explain how the cells are grouped in parallel. Obtain the condition for maximum current through an external resistor.
View SolutionThe current I drawn from the 5V source will be
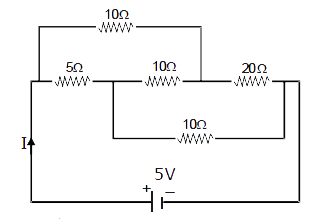
View SolutionThe current I drawn from the 5 V source will be
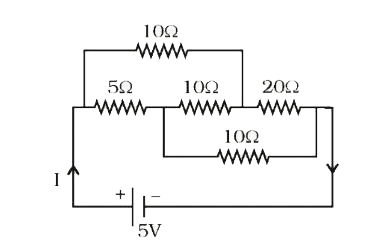
View SolutionA secondary cell after long use has an emf of 1.9 V and a large internal resistance of 380Ω. What maximum current can be drawn from the cell ? Could the cell drive the starting motor of a car ?
View Solution(a) Six lead-acid type of secondary cells each of emf 2.0 V and internal resistance 0.015 Ω are joined in series to provide a supply to a resistance of 8.5 Ω. What are the current drawn from the supply and its terminal voltage ?
(b) A secondary cell after long use has an emf of 1.9 V and a large internal resistance of 380 Ω . What maximum current can be drawn from the cell ? Could the cell drive the starting motor of a car?
View Solution(a) Six lead-acid type of secondary cells, each of emf 2.0 V and internal resistance 0.015Ω are joined in series to provide a supply to a resistance of 8.5Ω. What are the currents drawn from the supply, and its terminal voltage?
(b) A secondary cell after long use has an emf 1.9 V and a large internal resistance of 380Ω. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car?
View Solution(a) Six lead-acid type of secondary cells each of emf 2−0 V and internal resistance 0−015Ω are jouned in series to provide a supply to a resistance of 8−5Ω. What are the current drawn from the supply and its terminal voltage ?
(b) A secondary cells after long use has an emf of 1−9 V and a large internal resistance of 380Ω. What maximum current can be drawn from the cell ? Could the cell drive the starting motor of a car ?
View Solution
