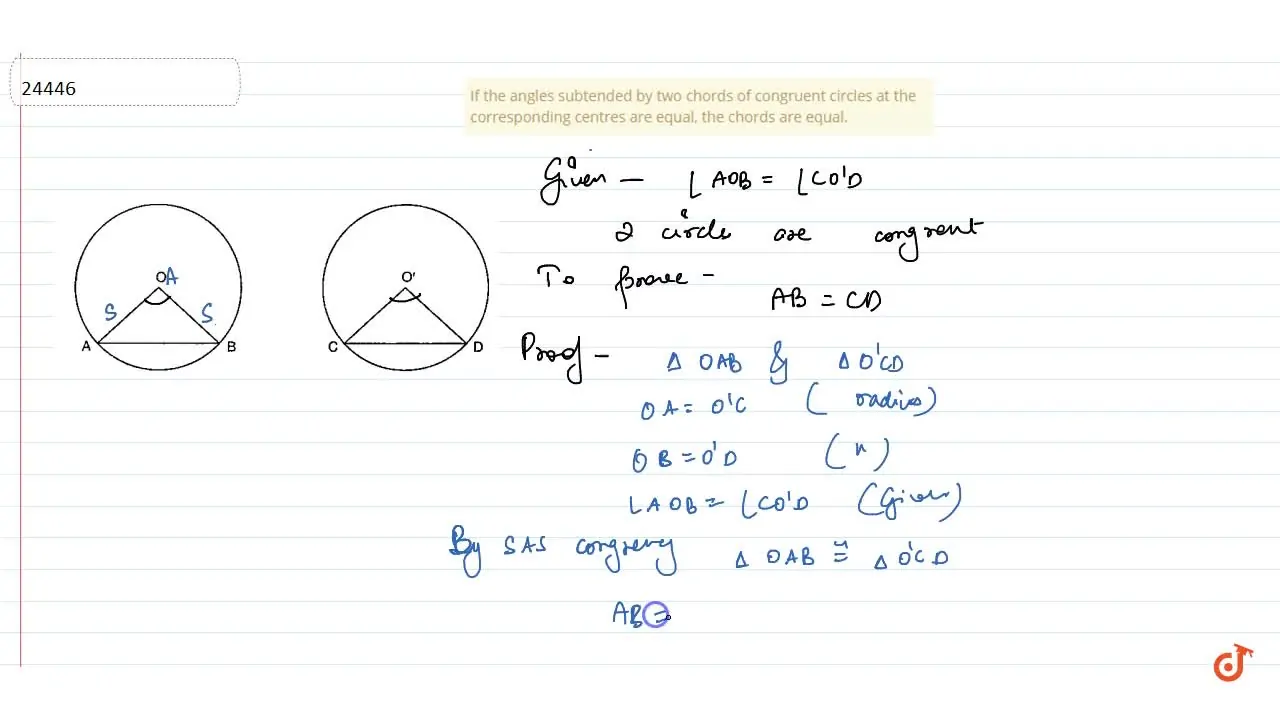
If the angles subtended by two chords of congruent circles at the corresponding centres are equal, the chords are equal.
Given: Two congruent circle C1 & C2 have equal angle at centres.
To Prove: Chords are equal.
Proof:
Let radius of these two circles are R
Now in ΔABC and ΔPQR
∠ABC=∠PQR (Given)
AB=PQ (Radius of congruent circles are equal)
BC=QR
ΔABC≅ΔPQR (SAS congruence rule)∴AC=PR (By CPCT)
Hence Proved.
Related Playlists
Similar Questions
IF the angle subtended by two chords of congruent circles at the corresponding centres are equal. Than the chords are equal
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, the chords are equal.
View SolutionState and prove that:
Theorem 10.2 : If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.View SolutionIf the angle subtended by two chords of a circle at the centre are equal; the chords are equal.
View SolutionChords of congruent circles which are equidistant from the corresponding centres, are equal.
View SolutionIf two chords of a congruent circle are equal; then their corresponding arcs are also equal.
View SolutionChords of congruent circles which are equidistant from the corresponding centres;are equal.
View SolutionIf two arcs of a circle are congruent; then corresponding chords are equal
View SolutionEqual chords of congruent circles are equidistant from the corresponding centres.
View SolutionEqual chord of congruent circles are equidistant from the corresponding centres.
View Solution