Question

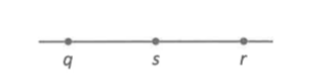
$0<p<q<r$
$\begin{array}{ccc}\text{Quantity A}& & \text{Quantity B}\\ \begin{array}{c}q-p\\ \text{+q}\\ \overline{2q-p}\end{array}& \text{(?)}& \begin{array}{c}r-q\\ \text{-q}\\ \overline{r-2q}\end{array}\end{array}$

Options

A. Quantity A is greater.
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the infromation given.

Answer

D

Explanation

To solve the problem, we need to analyze the two quantities given:

Quantity A: $$q-p+q=2q-p$$

Quantity B: $$r-q-q=r-2q$$

Given the conditions $$0<p<q<r$$, we will evaluate these quantities step by step.

Step 1: Express Quantity A
We start with Quantity A:
\( \text{Quantity A} = q - p + q = 2q - p \)

Step 2: Express Quantity B
Next, we express Quantity B:
\( \text{Quantity B} = r - q - q = r - 2q \)

Step 3: Compare the Two Quantities
Now we need to compare \( 2q - p \) and \( r - 2q \).

To do this, we can rearrange the comparison:
\( 2q - p \quad \text{and} \quad r - 2q \)
We want to see if \( 2q - p > r - 2q \), \( 2q - p < r - 2q \), or if they are equal.

Step 4: Rearranging the Inequality
Rearranging gives us:
\( 2q - p > r - 2q \implies 2q + 2q > r + p \implies 4q > r + p \)
\( 2q - p < r - 2q \implies 2q + 2q < r + p \implies 4q < r + p \)

Step 5: Analyze the Relationships
Given the constraints \( 0 < p < q < r \):
- If \( p \) is very small compared to \( r \), it is possible that \( 4q > r + p \).
- Conversely, if \( r \) is very large compared to \( q \), it could be that \( 4q < r + p \).

Step 6: Conclusion
Since we have seen that depending on the values of \( p, q, \) and \( r \), either quantity A or quantity B can be greater, we conclude that we cannot definitively determine the relationship between the two quantities based on the information given.

Thus, the answer is:
Option 4: The relationship cannot be determined from the information given.