Ten years ago, Brian was twice as old as Aubrey.
Quantity AQuantity BTwice Aubrey's age todayBrian's age today
The correct Answer is:Quantity A is greater.
To solve the problem step by step, let's define the ages of Brian and Aubrey based on the information provided.
Step 1: Define Variables
Let:
- A = Aubrey's current age
- B = Brian's current age
Step 2: Set Up the Equation from the Given Information
According to the problem, ten years ago, Brian was twice as old as Aubrey. This can be expressed as:
- Ten years ago, Aubrey's age = A−10
- Ten years ago, Brian's age = B−10
From the information given:
B−10=2(A−10)
Step 3: Simplify the Equation
Now, let's simplify the equation:
B−10=2A−20
Adding 10 to both sides gives:
B=2A−10
Step 4: Express the Quantities to Compare
Now we need to express the two quantities we are comparing:
- Quantity A: Twice Aubrey's age today
Quantity A=2A
- Quantity B: Brian's age today
Quantity B=B=2A−10
Step 5: Compare the Two Quantities
Now we need to compare 2A and 2A−10:
2Avs2A−10
Step 6: Determine the Relationship
To compare these, we can subtract 2A−10 from 2A:
2A−(2A−10)=10
Since 10>0, we conclude that:
2A>2A−10
Thus, Quantity A is greater than Quantity B.
Final Conclusion
Therefore, we can conclude that:
Quantity A>Quantity B
---
Let:
- A = Aubrey's current age
- B = Brian's current age
According to the problem, ten years ago, Brian was twice as old as Aubrey. This can be expressed as:
- Ten years ago, Aubrey's age = A−10
- Ten years ago, Brian's age = B−10
B−10=2(A−10)
Now, let's simplify the equation:
B−10=2A−20
Adding 10 to both sides gives:
B=2A−10
Now we need to express the two quantities we are comparing:
- Quantity A: Twice Aubrey's age today
Quantity A=2A
- Quantity B: Brian's age today
Quantity B=B=2A−10
Now we need to compare 2A and 2A−10:
2Avs2A−10
To compare these, we can subtract 2A−10 from 2A:
2A−(2A−10)=10
Since 10>0, we conclude that:
2A>2A−10
Thus, Quantity A is greater than Quantity B.
Therefore, we can conclude that:
Quantity A>Quantity B
Similar Questions
Knowledge Check
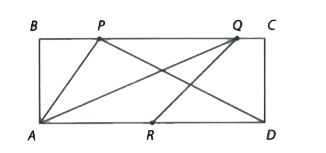
ABCD is a rectangle.
R is the midpoint of AD.
Quantity AQuantity BThe area of Triangle APDTwice the area of Triangle AQRAQuantity A is greater.BQuantity B is greater.CThe two quantities are equal.DThe relationship cannot be determined from the infromation given.Rectangle A has twice the area of Rectangle B. The width of Rectangle A is less than 1/2 the width of Rectangle B.
Quantity AQuantity BThe area of Rectangle AThe area of Rectangle B if itswidth is increased by morethen 2AQuantity A is greater.BQuantity B is greater.CThe two quantities are equal.DThe relationship cannot be determined from the infromation given.The circumference of Circle A is twice the circumference of circle B.
Quantity AQuantity BThe area of Circle ATwice the area of Circle BAQuantity A is greater.BQuantity B is greater.CThe two quantities are equal.DThe relationship cannot be determined from the infromation given.
Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
View SolutionTwo years ago, Salim was thrice as old as his daughter and six years later, he will be four year older than twice her age. How old are they now?
View SolutionFive years ago, A was thrice as old as B and 10 years later, A shall be twice as old as B. What are the present ages of A and B?
View SolutionOne year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son’s age. Find their present ages.
View SolutionTen years ago, a father was twelve times as old as his son and ten years hence, he will be twice as old as his son will be then. Find their present ages.
View Solution