Draw a coordinate plane and plot the following points :
x=6
The correct Answer is:(##GREMATMANPRPC14E01003_A01##)
To solve the problem of plotting the point x=6 on a coordinate plane, follow these steps:
1. Draw the Coordinate Plane:
- Start by drawing two perpendicular lines that intersect at a point. The horizontal line is called the x-axis, and the vertical line is called the y-axis. The point where they intersect is called the origin (0, 0).
2. Label the Axes:
- Mark the positive direction of the x-axis to the right of the origin and the negative direction to the left. Similarly, mark the positive direction of the y-axis upwards and the negative direction downwards.
3. Choose a Scale:
- Decide on a scale for the axes. For example, you can mark each unit as 1 unit apart. You can also choose to mark every 2 units for easier plotting. For this example, let’s mark every 2 units on the x-axis: 2, 4, 6, 8, 10 on the positive side and -2, -4, -6 on the negative side.
4. Locate the Point x=6:
- Since the equation is x=6, this means that the x-coordinate is fixed at 6. The y-coordinate can be any value. Therefore, you can plot several points where x=6 and y can take any value (for example, y=0,1,2,−1,−2, etc.).
5. Plot the Point:
- For simplicity, let’s plot the point where y=0. This gives us the point (6, 0). Mark this point on the coordinate plane.
6. Draw the Line:
- To represent the equation x=6, draw a vertical line through the point (6, 0) extending upwards and downwards. This line indicates that for any value of y, the x-coordinate remains 6.
Final Representation:
- The vertical line you drew represents all points where x=6. Some example points on this line are (6, 1), (6, -1), (6, 2), (6, -2), etc.
- Start by drawing two perpendicular lines that intersect at a point. The horizontal line is called the x-axis, and the vertical line is called the y-axis. The point where they intersect is called the origin (0, 0).
- Mark the positive direction of the x-axis to the right of the origin and the negative direction to the left. Similarly, mark the positive direction of the y-axis upwards and the negative direction downwards.
- Decide on a scale for the axes. For example, you can mark each unit as 1 unit apart. You can also choose to mark every 2 units for easier plotting. For this example, let’s mark every 2 units on the x-axis: 2, 4, 6, 8, 10 on the positive side and -2, -4, -6 on the negative side.
- Since the equation is x=6, this means that the x-coordinate is fixed at 6. The y-coordinate can be any value. Therefore, you can plot several points where x=6 and y can take any value (for example, y=0,1,2,−1,−2, etc.).
- For simplicity, let’s plot the point where y=0. This gives us the point (6, 0). Mark this point on the coordinate plane.
- To represent the equation x=6, draw a vertical line through the point (6, 0) extending upwards and downwards. This line indicates that for any value of y, the x-coordinate remains 6.
- The vertical line you drew represents all points where x=6. Some example points on this line are (6, 1), (6, -1), (6, 2), (6, -2), etc.
Similar Questions
Knowledge Check
What is the y-intercept of the line in the standard (x,y) coordinate plane that goes through the points (-3,6) and (3,2) ?
A0B2C4D6Which point on the coordinate plane shown here is indicated by the following coordinates?
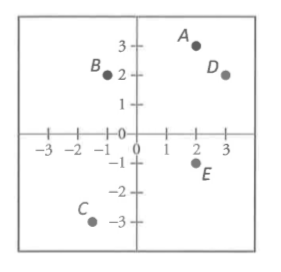 A(2,−1)B(−1.5,−3)C(−1,2)D(3,2)
A(2,−1)B(−1.5,−3)C(−1,2)D(3,2)In the standard (x,y) coordinate plane below, the points (0,0), (10,0), (13,6) and (3,6) are the vertices of a parallelogram. What is the area, in square coordinate units, of the parallelogram?
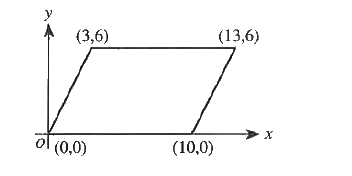 A30B60C30√3D30√5
A30B60C30√3D30√5
Draw a coordinate plane and graph the line y=2x−4. Identify the slope and the y - intercept.
View SolutionA parallelopiped is formed by planes drawn through the points (1, 2, 3) and
(6, 8, 18) parallel to the coordinate planes then which of the following is not
the length of an edge of the rectangular
parallelpiped
View SolutionA variable plane at a constant distance p from the origin meets the coordinate axes in points A,B and C respectively.Through these points , planes are drawn parallel to the coordinate planes, show that locus of the point of intersection is 1x2+1y2+1z2=1p2
View SolutionA rectangular parallelopiped is formed by drawing planes through the points (1,2,5)and(−1,−1,−1) parallel to the coordinate planes. Find the length of the diagnol of the parallelopiped.
View SolutionWhen points A and B (-3, 4) are graphed in the standard (x,y) coordinate plane below, the midpoint of ¯¯¯¯¯¯AB will be (1,2). What will be the coordinate of point A?

View Solution
