A square field has an area of 400 square meters. Posts are set at all corners of the field. What is the longest distance between any two posts?
The correct Answer is:20√2 meters
To solve the problem of finding the longest distance between any two posts set at the corners of a square field with an area of 400 square meters, we can follow these steps:
1. Understand the Problem: We have a square field with posts at each corner. We need to find the longest distance between any two posts.
2. Draw a Diagram: Visualize the square field. Label the corners as A, B, C, and D. The posts are located at these corners.
3. Identify the Length of the Side: The area of the square field is given as 400 square meters. The formula for the area of a square is:
Area=side2
Therefore, we can find the length of each side (s) by taking the square root of the area:
s=√400=20 meters
4. Calculate the Diagonal: The longest distance between any two posts will be the diagonal of the square. The formula for the diagonal (d) of a square in terms of its side length is:
d=s√2
Substituting the value of s:
d=20√2 meters
5. Conclusion: The longest distance between any two posts, which are located at opposite corners of the square, is:
Longest distance=20√2 meters
Final Answer:
The longest distance between any two posts is 20√2 meters.
Area=side2
Therefore, we can find the length of each side (s) by taking the square root of the area:
s=√400=20 meters
d=s√2
Substituting the value of s:
d=20√2 meters
Longest distance=20√2 meters
The longest distance between any two posts is 20√2 meters.
Similar Questions
Knowledge Check
A rectangle has a perimeter of 16 meters and an area of 15 square meters. What is the longest of the side lengths, in meters, of the rectangle?
A3B5C10D15A square field measures 10 meters by 10 meters. Ten students each mark off a randomly selected region of the field, each region is square and has side lengths of 1 meter, and no two regions overlap. The students count the earthworms contained in the soil to a depth of 5 centimeters beneath the ground’s surface in each region. The results are shown in the table below.
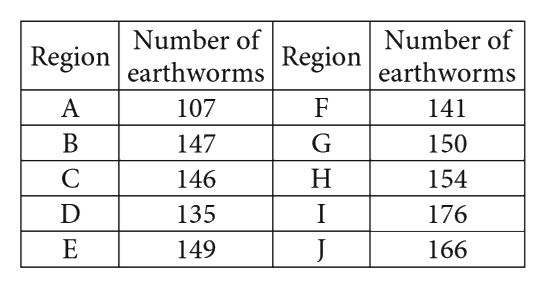
Which of the following is a reasonable approximation of the number of earthworms to a depth of 5 centimeters beneath the ground’s surface in the entire field?A150B1500C15000D150000
The side of a square field is 65m. What is the length of the fence required all around it?
View SolutionA circular field has a perimeter of 650 m. A square plot having its vertices on the circumference of the field is marked in the field. Calculate the area of the square plot.
View SolutionThe area of a square field is 1 hectare . What is its perimeter ?
View SolutionFour spheres A, B, C, D, each of mass m and diameter 2 a are placed with their centres at die four corners of a square of side b. What is the moment of inertia of the system about any side of the square ?
View SolutionThe area of a square field is 325 m2. Find the approximate length of one side of the field.
View SolutionFind the area of a square field if its each side is 1034 m long.
View Solution
