A satellite is to be placed in equatorial geostationary orbit around earth for communication.
(a) Calculate height of such a satellite.
(b) Find out the minimum number of satellites that are needed to cover entire earth so that at least one satellites is visible from any point on the equator.
[M=6×1024kg,R=6400km,T=24h,G=6.67×10−11SIunits]
Consider the adjacent diagram
Given, mass of the earth M=6×1024kg
Radius of the earth, R=6400km=6.4×106m
Time period T=24h
=24×60×7=60=86400s
G=667×10−11N−m2/kg2
(a) Time period T=2π√(R+h)3GM [.:v0=√GMR+h and T=2π(R+h)v0]
⇒T2=4π2(R+h)3GM⇒(R+h)3=T2GM4π2
⇒R+h=(T2GM4π2)1/3⇒h=(T2GM4π2)1/3−R
⇒h=[(24×60×60)2×6.67×10−11×6×10244×(3.14)2]1/3−64×106
=4.23×107−6.4×106
=(42.3−6.4)×106
=35.0×106m
=3.59×107m
(b) If satellite is at height h from the earth's surface, then according to the diagram.
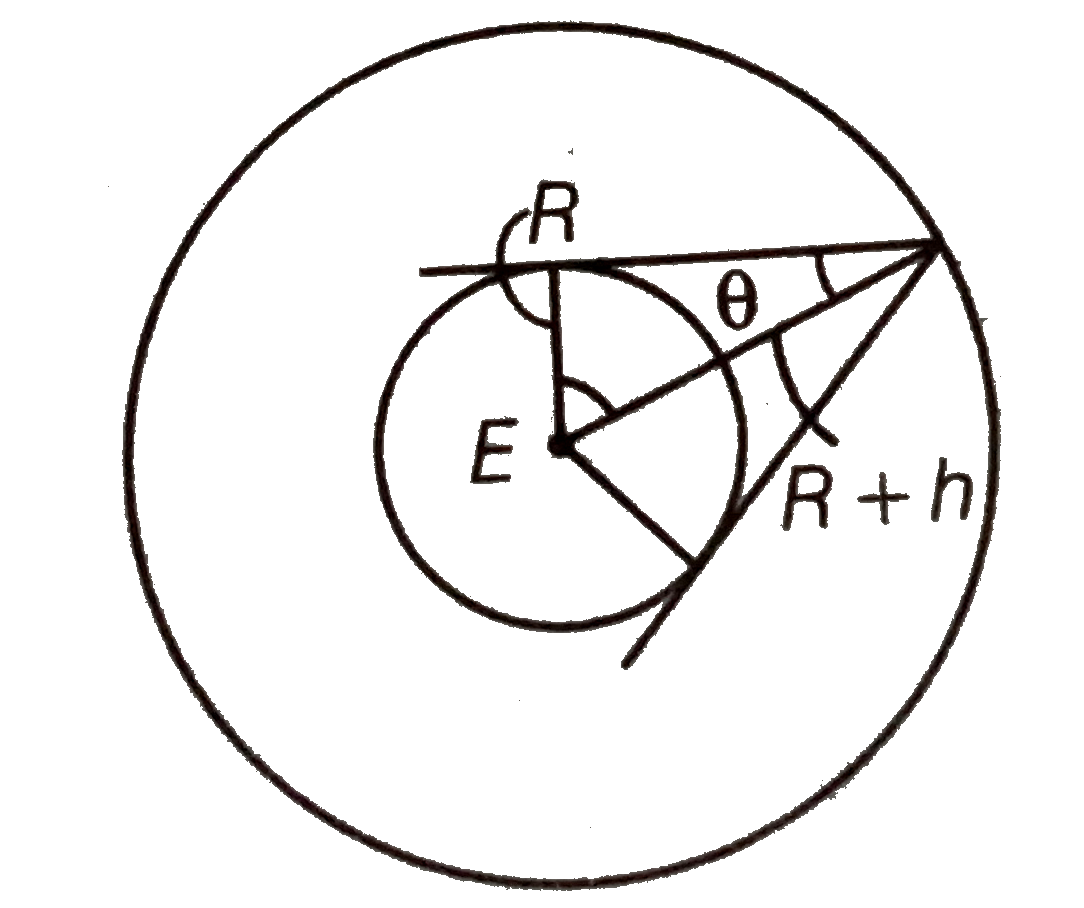
cosθ=RR+h=1(1+hR)=1(1+3.59×1076.4×106)
=11+5.61=16.61=0.1513=cos81∘18'
θ=81∘18'
∴2θ=2×(81∘18')=162∘36'
If n is the number of satellites needed to cover entire the earth, then
n=360∘2θ=360∘162∘36'=2.31<br>:. Minimum 3 satellites are required to cover entire the earth
Topper's Solved these Questions
Similar Questions
A geostationary satellite orbits the Earth at a height of nearly 36,000km from the surface of earth. What is the potential due to earth's gravity at the site of tthis satllite ? (Take the potential energy at infinity to be zero). Mass of the Earth =6.0×1024kg, radius =6400km,G=6.67×10−11Nm2/kg2.
View SolutionA satellite is orbiting around earth with its orbit radius 16 times as great as that of parking satellite. What is the period of this satellite.
View Solution
Knowledge Check
A geostationary satellite revolves around the earth from
Anorth to southBsouth to northCwest to eastDeast to westMinimum number of geostationary satellites needed for stallite communication is
A1B2C3D4A satellite can be in a geostationary orbit around earth in an orbit of radius r. If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit aroun earth radius
Ar2Br2√2Cr(4)1/3Dr(2)1/3
A satellite is revolving in circular orbit of radius r around the earth of mass M. Time of revolution of satellite is
View SolutionA satellite is orbiting around the earth at a mean radius of 16 times that of the geostationary orbit. What is the period of the satellite ?
View SolutionA satellite can be in a geostationary orbit around earth at a distance r from the centrer. If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit around if its distance from the centre is
View SolutionWhat is the approximate height of any geostationary satellite from earth’s surface (in km)?
View SolutionA geostationary satellite orbits around the earth in a circular orbit of radius 3600km. Then the time period of satellite orbiting =2600km above the earth's surface (Rearth=6400km) will appoximetely be
View Solution

