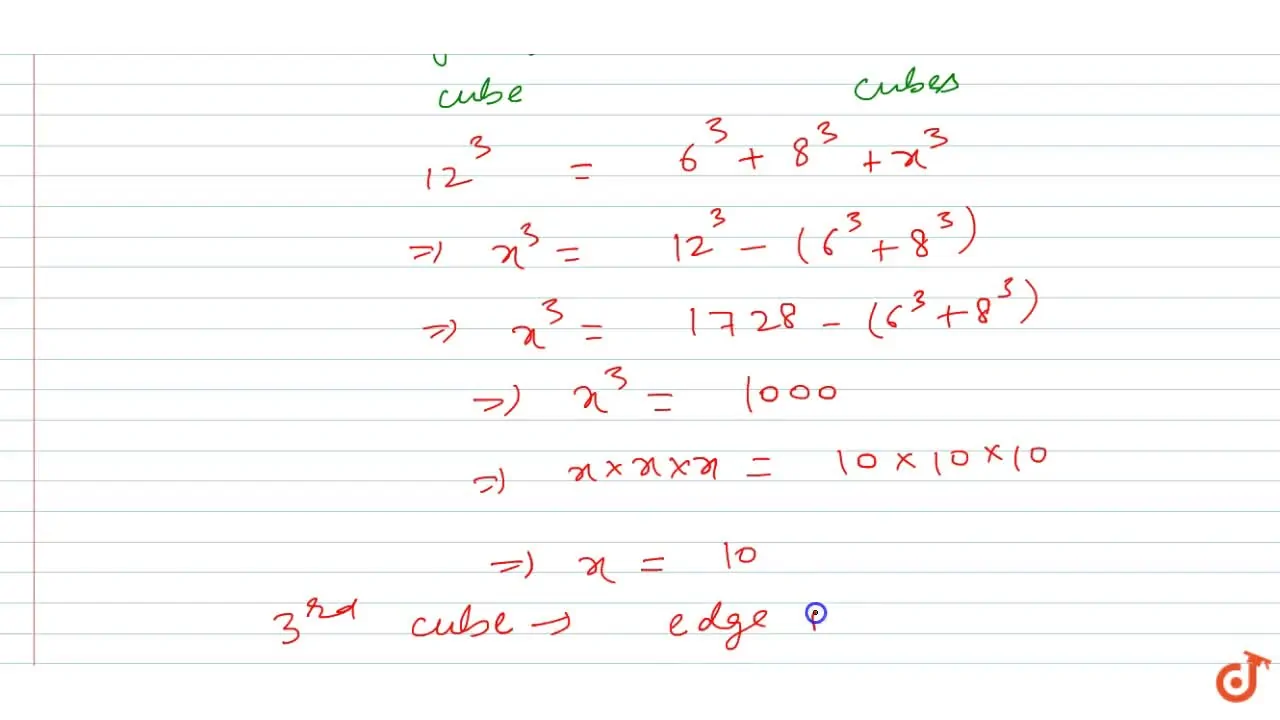A metal cube of edge 12cm is melted and formed into three smaller cubes. If the edges of the two smaller cubes are 6cm and 8cm, find the edge of the third smaller cube.
Volume of bigger cube= volume of 3 smaller cubes
123=63+83+x3
x3=123−(63+83)
x3=10⋅10⋅10
x=10
3rd cube -> edge is 10 cm.
Related Playlists
Similar Questions
A wax cube of edge 6 cm is melted and formed into three smaller cubes. If the edges of two smaller cubes are 3 cm and 4 cm . What is the edge of the third smaller cube?
View SolutionA metal cube of edge 9 cm is melted and made into three smaller cubes.If the edges of two smaller cubes are 1cm and 6 cm find the edge of the third smaller cube.
View SolutionA metal cube of edge 310 m is melted and formed into three smaller cubes. If the edges of the two smaller cubes are 15m and 14m, find the edge of the third smaller cube.
View SolutionA metal cube of edge 310 m is melted and formed into three smaller cubes. If the edges of the two smaller cubes are 15 m and 14 m, find the edge of the third smaller cube.
View SolutionA metal cube of edge 12 cm, is melted and casted into three small cubes. If the edges of two small cubes be 6 cm and 8 cm, then the edge of the third small cube is
View SolutionA metal cube of edge 12 cm, is melted and casted into three small cubes. If the edges of two small cubes be 6 cm and 8 cm, then the edge of the third small cube is
View SolutionA metal cube of 9 cm edge is melted and recast into three smaller cubes. If the edge of two of the smaller cubes are 1 cm and 6 cm. Find the edge of the third cube.
View SolutionA metal solid cube of edge 24 cm is melted and made into three small cubes. If the edges of two small cubes are 12 cm and 16 cm, then what is the surface area of the third small cube?
View SolutionA metal cube of volume 2933 cm^(3) is melted and three smaller cubes are made out of it.If the edges of two smaller cubes are 5cm and 4cm ,find the edge of the third smaller cube.
View SolutionA metal cube of edge 3√2√5 m is melted and formed into three smaller cubes. If the edges of the two smaller cubes are 3√10mand√5√2m, find the edge of the third smaller cube.
View Solution