How will you calculate work done on an ideal gas in a compression, when change in pressure is carried out in infinite steps?
To calculate the work done on an ideal gas during a compression process where the change in pressure occurs in infinite steps (reversible process), we can follow these steps:
1. Understand the Process: Recognize that in a reversible compression of an ideal gas, the process occurs in such a way that the gas is always in equilibrium with its surroundings. This means that the pressure of the gas changes continuously and infinitesimally.
2. Identify the Initial and Final States: Let the initial state of the gas be defined by the initial pressure Pi and volume Vi, and the final state by the final pressure Pf and volume Vf.
3. Use the Ideal Gas Law: The ideal gas law states that PV=nRT, where n is the number of moles of gas and R is the ideal gas constant. This relationship will help us understand how pressure and volume change during the process.
4. Set Up the Work Done Formula: The work done W on the gas during a reversible process can be expressed as:
W=−∫VfViPdV
The negative sign indicates that work is done on the gas (compression).
5. Express Pressure as a Function of Volume: Since we are dealing with a reversible process, we can express pressure P as a function of volume V. For an isothermal process (constant temperature), the relationship can be described by:
P=nRTV
This leads to a rectangular hyperbola when plotted on a PV graph.
6. Integrate to Find Work Done: Substitute the expression for P into the work done formula:
W=−∫VfVinRTVdV
This integral can be solved as follows:
W=−nRT∫VfVi1VdV=−nRT(lnV)VfVi
W=−nRT(lnVf−lnVi)=−nRTln(VfVi)
7. Final Expression for Work Done: The final expression for the work done on the gas during reversible compression is:
W=nRTln(ViVf)
W=−∫VfViPdV
The negative sign indicates that work is done on the gas (compression).
P=nRTV
This leads to a rectangular hyperbola when plotted on a PV graph.
W=−∫VfVinRTVdV
This integral can be solved as follows:
W=−nRT∫VfVi1VdV=−nRT(lnV)VfVi
W=−nRT(lnVf−lnVi)=−nRTln(VfVi)
W=nRTln(ViVf)
Similar Questions
Knowledge Check
When an ideal gas is compressed isothermally then its pressure increase because:
Aits potential energy decreasesBits kinetic energy increases and molecules move apartCits number of collisions per unitl area with walls of container increasesDmolecules energy increasesWhen an ideal gas is compressed isothermally then its pressure increase because:
Aits potential energy decreasesBits kinetic energy increases and molecules move partCits number of collisions per unit area with walls of container increasesDMolecular energy increasesThe work done when an ideal gas is compressed isothermally by 1 litre against a constant atmospheric pressure is
A1 JB-1 JC+ 0.1013 kJD-1013 J
What will be the work done on an ideal gas enclosed in a cylinder, when it is compressed by a constant external pressure pext , in a single step as shown in figure? Explain graphically.
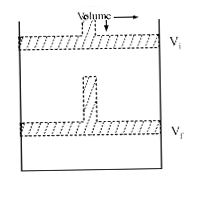
View SolutionWhat will be the work done on an ideal gas enclosed in a cylinder, when it is compressed by a constant external pressure pext , in a single step as shown in figure? Explain graphically.
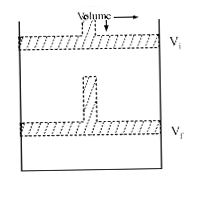
View SolutionCalculate the work done when one mole of an ideal monoatomic gas is compressed adiabatically. The initial pressure and volume of the gas are 105N/m2 and 6 litre respectively. The final volume of the gas is 2litres. Molar specific heat of the gas at constant volume is 3R/2.
View SolutionThe work done in an isothermal reversible change involving an ideal gas is given by
View SolutionPressure volume (PV) work done by an ideal gas system at constant volume is
View Solution


