Question

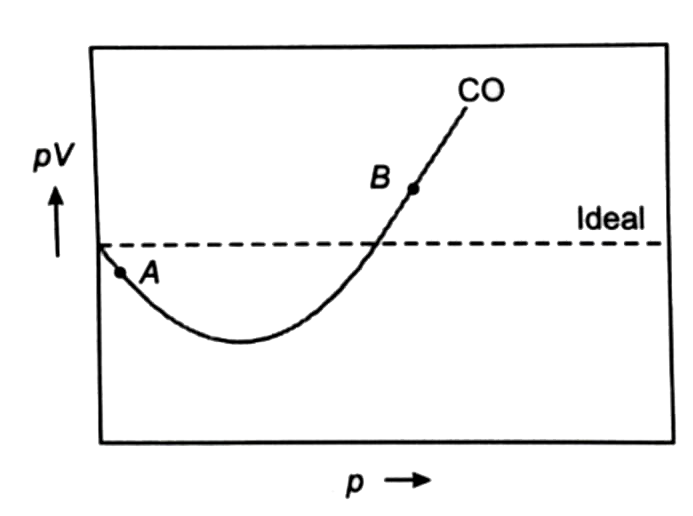
In the above Question, near the point B, compressibility factor Z is about :

Options

A. `(1-(Pb)/(RT))`
B. 1
C. `(1 + (Pb)/(RT))`
D. `(1-(a)/(RTV))`

Answer

C

Explanation

To determine the compressibility factor $$Z$$ near point B for carbon monoxide, we can follow these steps:

Step 1: Understand the Compressibility Factor
The compressibility factor \( Z \) is defined as the ratio of the molar volume of a real gas to the molar volume of an ideal gas at the same temperature and pressure. It indicates how much a real gas deviates from ideal gas behavior. The formula is given by:
\( Z = \frac{PV}{nRT} \)

Step 2: Use the Van der Waals Equation
The Van der Waals equation for real gases is:
\( \left(P + \frac{a n^2}{V^2}\right)(V - nb) = nRT \)
For our case, we consider \( n = 1 \) (1 mole of carbon monoxide), which simplifies the equation to:
\( \left(P + \frac{a}{V^2}\right)(V - b) = RT \)

Step 3: Analyze Conditions at High Pressure
At high pressures (near point B), the term \( \frac{a}{V^2} \) becomes negligible compared to \( P \). Thus, we can ignore the pressure correction term:
\( P(V - b) = RT \)

Step 4: Rearrange the Equation
Rearranging the equation gives us:
\( PV - Pb = RT \)
This can be rewritten as:
\( PV = RT + Pb \)

Step 5: Divide by RT
Now, divide the entire equation by \( RT \):
\( \frac{PV}{RT} = 1 + \frac{Pb}{RT} \)

Step 6: Identify the Compressibility Factor
From the above equation, we can identify the compressibility factor \( Z \):
\( Z = \frac{PV}{RT} = 1 + \frac{Pb}{RT} \)

Conclusion
Thus, near point B, the compressibility factor \( Z \) is given by:
\( Z = 1 + \frac{Pb}{RT} \)