1c∫bcacf(xc)dx=
c∫baf(cx)dx
1c∫baf(xc)dx
1c∫baf(cx)dx
c∫baf(xc)dx
The correct Answer is:A
Step by step video & text solution for (1)/(c )int_(ac)^(bc)f((x)/(c ))dx= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
1c∫bcacf(xc)dx=
A1c∫baf(x)dxB∫baf(x)dxCc∫baf(x)dxD∫bc2ac2f(x)dx1c∫baf(xc)dx=
A1c∫baf(x)dxB∫baf(x)dxCc∫baf(x)dxD∫bc2ax2f(x)dxFor every function f (x) which is twice differentiable , these will be good approximation of
∫baf(x)dx=(b−a2){f(a)+f(b)}, for more acutare results for c∈(a,b),F(c)=c−a2[f(a)−f(c)]+b−c2[f(b)−f(c)]
When c=a+b2
∫baf(x)dx=b−a4{f(a)+f(b)+2f(c)}dx
Good approximation of ∫π/20sinxdx,isAπ/4Bπ(√2+1)/4Cπ(√2+1)/8Dπ8
STATEMENT-1 : ∫5π−2πcot−1(tanx)dx=7π22
and
STATEMENT-2 : ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx, a<c<b
View SolutionSTATEMENT 1: ∫π0sin100xcos99xdxis z ero . STATEMENT 2: ∫baf(x)dx=∫b+ca+cf(x−c)dx,and for odd function, ∫a−af(x)dx=0
View Solution∫b+ca+cf(x)dx is equal to:
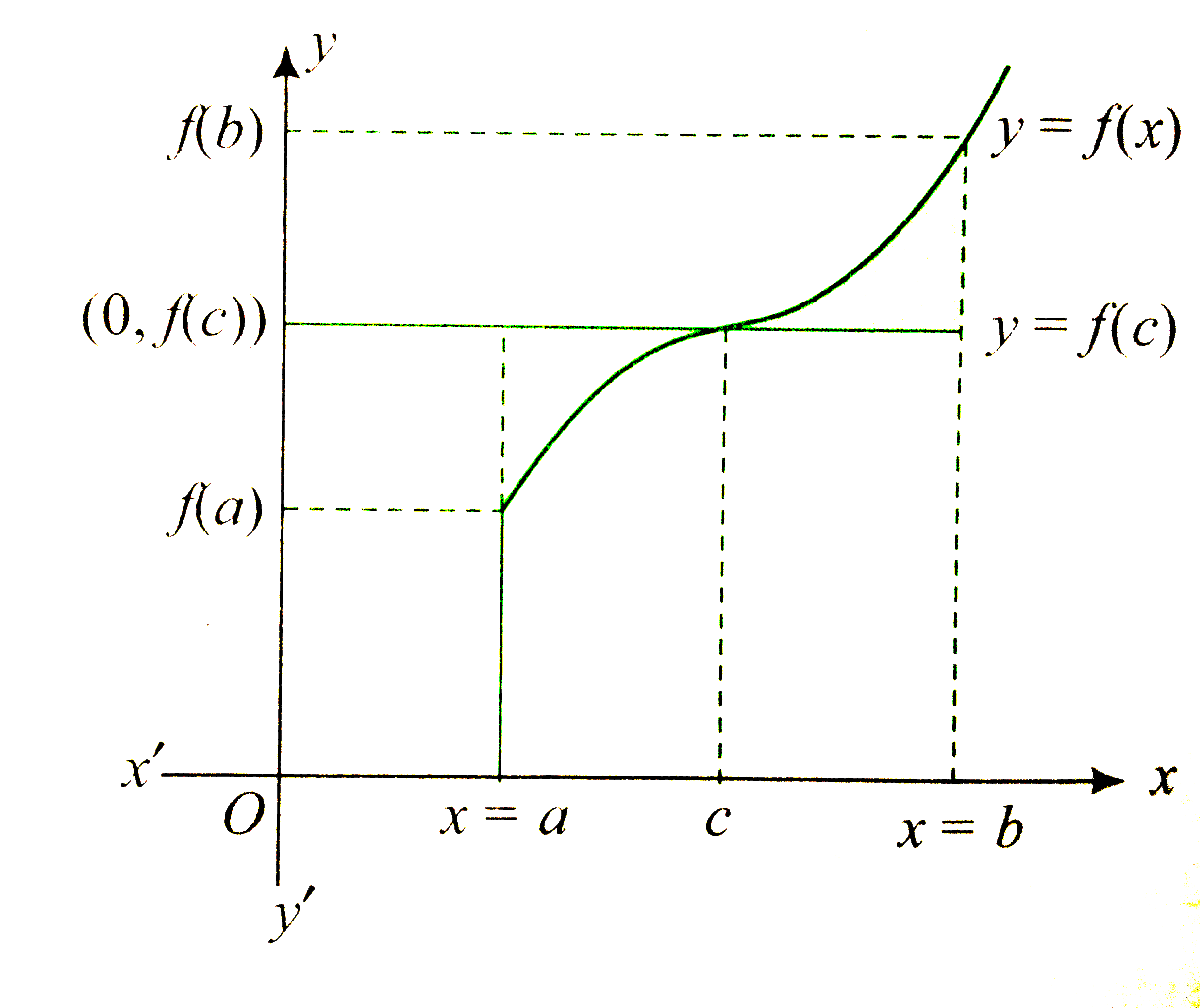
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
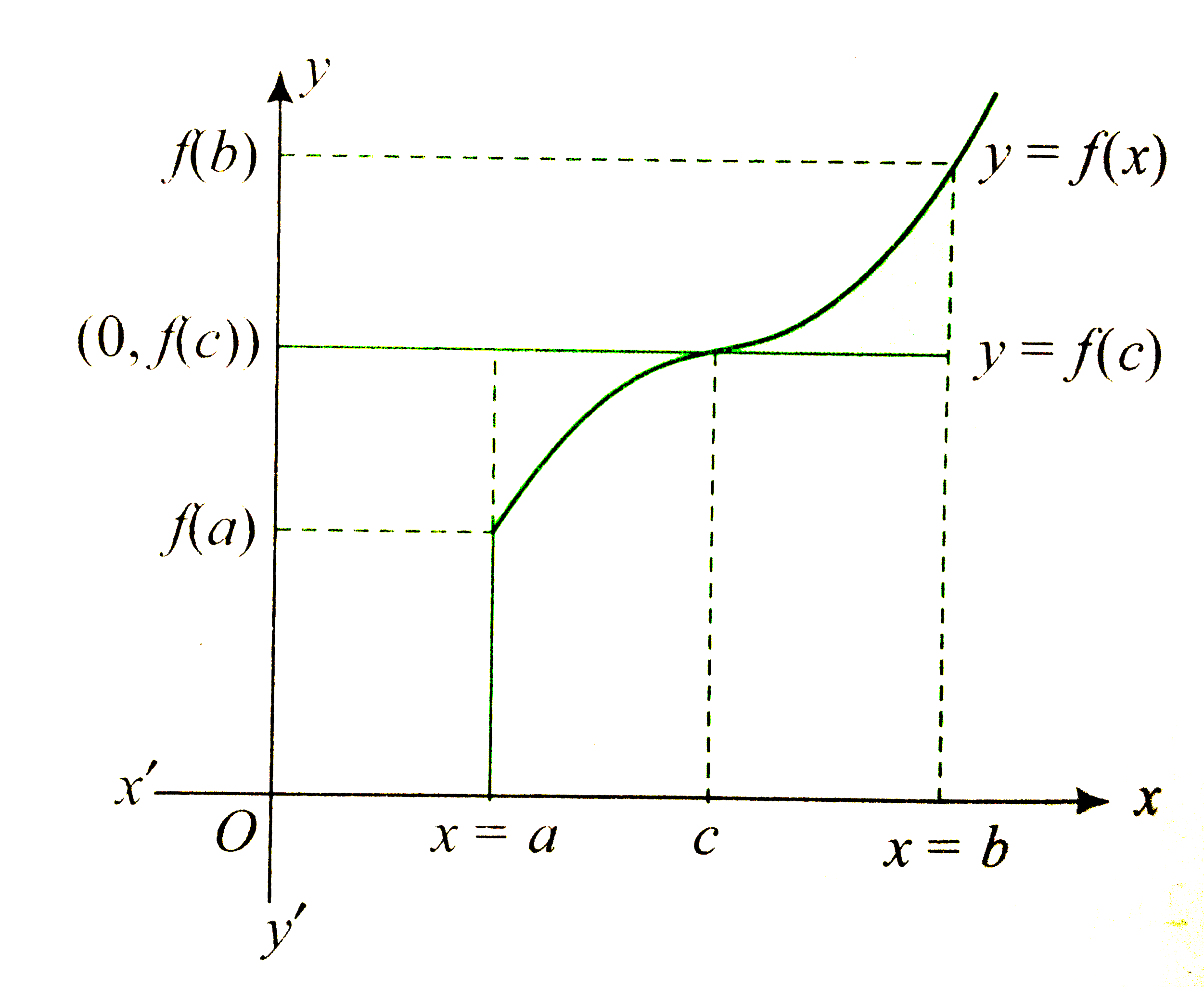
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area enclosed by f(x)=sinx+cosx,y=a between two consecutive points of extremum is minimum, then the value of a is
View Solution
